Геометрия: ABCD параллелограмм. Найти его площадь РЕШЕНИЕ

ABCD параллелограмм. Найти его площадь РЕШЕНИЕ

👇

Увидеть ответ

Ответ:

LolaTi

14.12.2020

Т.к. АВСD параллелограмм, то АD = BC = 10.

Проведём высоту BH.

Тр. АВН - прямоугольный. Угол ВАН = 30° (т.к. сумма двух углов параллелограмма равна 180°, отсюда 180 - 150 = 30° = углу А).

В тр.АВН катет лежащий против угла в 30° равен половине гипотенузы ВН = 1/2AB. АВ = АD = 10, значит ВН = 5.

Площадь ABCD = 10 × 5 = 50

Объяснение:

Чё за рофлы, чел?

У тя куча заданий по математике решено и ты - светило науки.

4,6(51 оценок)

Ответ:

mashakovalak234

14.12.2020

S=50 квадратных единиц.

Объяснение:

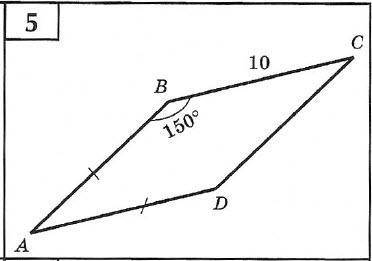
Дано: ABCD параллелограмм, АВ=AD, ВС=10, ∠АВС=150°.

Найти: S - площадь ABCD.

Решение: по формуле нахождения площади параллелограмма

S=AB*BC*sin∠В

Подставим в вышеуказанную формулу известные значения:

S=AB*BC*sin150°

S=AB*10*0,5

S=AB*5

По определению параллелограмма BC=AD. То есть AD=10 единиц. Так как по условию АВ=AD, то АВ=10 единицам. Подставим в последнюю формулу полученное значение

S=10*5

S=50 квадратных единиц.

4,4(100 оценок)

Открыть все ответы

Ответ:

myzroman

14.12.2020

В начале построим рисунок, который приложу вложением. Для наглядности соединим т. О поочерёдно с точками A, B, C, D. Получаем пирамиду с вершиной в т. O, в основании которой лежит квадрат ABCD.
Первый вопрос: 1). Докажем, что плоскость ABCD параллельна плоскости A1B1C1D1. Для этого построим пары диагоналей AC, BD, а также A1C1, B1D1.
2). Теперь рассмотрим треугольник OBD. Прямая B1D1 параллельна прямой BD, как средняя линия треугольника OBD, т.к. B1D1 соединяет середины его сторон B1 и D1 (эти точки середины по условию).
3). Теперь рассмотрим треугольник OAC. Прямая A1C1 параллельна прямой AC, как средняя линия треугольника OAC, т.к. A1C1 соединяет середины его сторон A1 и C1 (эти точки середины по условию).
4). Тогда получаем, что две пересекающиеся прямые AC и BD плоскости ABCD параллельны двум пересекающимся прямым A1C1 и B1D1 плоскости A1B1C1D1, а из этого, по теореме о параллельности двух плоскостей, следует, что плоскости ABCD и A1B1C1D1 параллельны, что и требовалось доказать.
Второй вопрос: 1). Рассмотрим треугольник OBA. B1A1 - средняя линия треугольника OBA, т.к. соединяет середины сторон OB и OA (B1 и D1 середины по условию). Тогда B1A1=1/2 AB=10/2=5.
2). Аналогично B1C1 - средняя линия треугольника BC, C1D1 - средняя линия треугольника CD, A1D1 - средняя линия треугольника AD.
3). Тогда, B1C1=5, C1D1=5, A1D1=5.
4). Периметр A1B1C1D1=B1C1+C1D1+A1D1+B1A1=5+5+5+5=20

Квадраь abcd со стороной 10 см и точка o не лежат в одной плоскости точки a1b1c1d1 являются середина

Квадраь abcd со стороной 10 см и точка o не лежат в одной плоскости точки a1b1c1d1 являются середина

4,6(50 оценок)

Ответ:

pipia07

14.12.2020

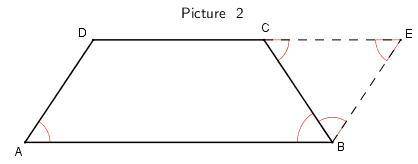
Предоставлю точно также два решения только другой метод(более рационален). Из вершины D продлим сторону до пересечения на продлении стороны BC, так что AB ║ DE, т.е. ABED — параллелограмм.

∠A = ∠E = 60° (противоположные углы у параллелограмма равны)

Так как AB = CD ⇒ ED = CD ⇒ ∠ECD = ∠CED = ∠CDE = 60°, т.е. треугольник CDE — равносторонний ⇒ CD = CE = ED = 32

Тогда AD = BC + CE = 20 + 32 = 52

P = 20 + 32 + 32 + 52 = 136

Рисунок 2.

Аналогично решению из рисунка 1, достроим до параллелограмма ADEB, AD ║ EB, мы имеем что ΔCEB - равносторонний, т.е. CE = CB = EB = 20, тогда CD = AB - CE = 32 - 20 = 12.

P = 12 + 20 + 20 + 32 = 84