Question

Дан равнобедренный треугольник, основание равно 18 см, высота проведенная к основания равна 12 см. найдите радиус а) вписанной окружности, б) описанной окружности

Answer 1

Высота в равнобедренном треугольнике делит его на два равных прмоугольных треугольника. При этом, высота разбивает основание не две равные части, и они равны 18/2=9 см. В треугольнике ВДС по теореме Пифагора

 $BC= \sqrt{BD^{2}+BC^{2}$

$BC= \sqrt{12^{2}+9^{2}\\$

$BC= \sqrt{225}\\$

ВС=15.

Так как треугольник равнобедренный, то АС=ВС=15.

Радиус вписанной окружности -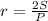 $r=\frac{2S}{P}$ , радиус описанной окружности - [tex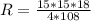$R=\frac{15*15*18}{4*108}$]R=\frac{abc}{4S}[/tex].

Периметр треугольника равен 15*2+18=48 см. Площадь треугольника по формуле Герона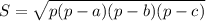 $S=\sqrt{p(p-a)(p-b)(p-c)$, гдер - полупериметр, равный 48/2=24 см.

$S=\sqrt{(24*(24-15)^{2}(24-18)$

$S=\sqrt{(6*4*9^{2}*6$

S=6*2*9=108 см^2

Теперь мы можем найти радиусы:

$r=\frac{2*108}{48}$

r=4.5 cм

$R=\frac{15*15*18}{4*108}$

R=9.375 см.

ответ: радиус вписанной окружности - 4,5см, радиус оаписанной окружности 9,375 см. ;)