AK=5√6 см, KB=10 см
Объяснение:
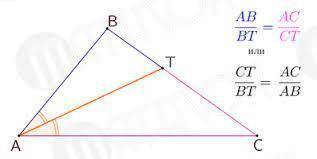
Теорема биссектрисы прикреплена в рисунке. По ней мы имеем:
BK/KC=AB/AC=20/10=2
BK=2KC; CB=BK+KC=15⇒2KC+KC=15
3KC=15; KC=15/3=5 см
BK=BC-KC=15-5=10 см
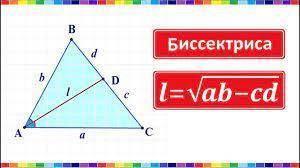
Вторая теорема биссектрисы также прикреплена к ответу. По ней имеем:
AK=√AB*AC-BK*KC=√200-50=√150=√25*√6=5√6
Далее идут доказательства верности ответа другими, тяжёлыми для понимания теоремами. Их не желательно употреблять, они здесь только ради утверждения компетентности моего 2-го ответа. (Ну и для того, чтобы похвастаться знаниями тоже)
Проверим ответ по теореме Стюарта:
AK²*BC=AB²*KC + AC²*BK - BC*KC*BK
AK²*15=400*5 + 100*10 - 15*10*5=2250
AK²=2250/15=150
AK=√150=√25*√6=5√6
ЧТД
Третья формула для нахождения биссектрисы
AK²=AB² * KC/BC + AC² * BK/BC - BK*KC
AK²=2000/15+1000/15-50=200-50=150
AK=√150=√25*√6=5√6
ЧТД
Основания трапеции равны 26 см и 16 см.
Объяснение:
Пусть дана трапеция ABCD со средней линией EF.
Диагонали трапеции делят среднюю линию на три части:
EM, MN и NF, причем MN = 5 см.
Отрезки ЕМ и NF - средние линии треугольников АВС и DBC, так как они параллельны стороне ВС и соединяют середины двух других сторон.
Следовательно, ЕМ = NF = BC/2. Но ЕМ+NF = EF - MN = 21-5 =16см.
Тогда ЕМ = NF = 8см =>
BC = 16cм.
Средняя линия равна полусумме оснований. =>
(AD+BC)/2 = 21 cм (дано) =>
AD = 21·2 -BC = 26 см.

Площадь кола=29,16П
радиус=5,4