Дано:
ABCD-параллелограмм
BC=31
∠C=45°
AB=BD
Найти: Sabcd
1. У параллелограмма противоположные углы равны, значит ∠C=∠A=45°
2. Проведём высоту с вершины B к основанию AD (назовем ее BH)
3. ∠B=180°-90°-45°=45°. Значит, ΔABH-равнобедренный
4. Рассмотрим ΔBHD. ∠HBD=45°, так как противоположные углы параллелограмма равны. Сумма углов параллелограмма равна 360°. ∠B=∠D=360°-45°-45°/2 =135°. Весь ∠B=135°, его части (∠ABH и ∠DBC=45°, значит ∠HBD=135°-45°-45°=45°)
5. Так как ∠HBD=45°, ∠BHD=45°, то ∠BDH=180°-90°-45°=45°.
6. Рассмотрим ΔABD-он равнобедренный, значит BH- и высота, и медиана, и биссектриса. AH=HD
7. BC=AD=31 (по определению параллелограмма)
8. AH=31/2=15,5
9. Так как ΔABH-равнобедренный, то BH=AH=15,5
10. Sabcd=AD*BH=31*15,5=480,5
ответ: Sabcd=480,5
Доказательство в объяснении.
Объяснение:
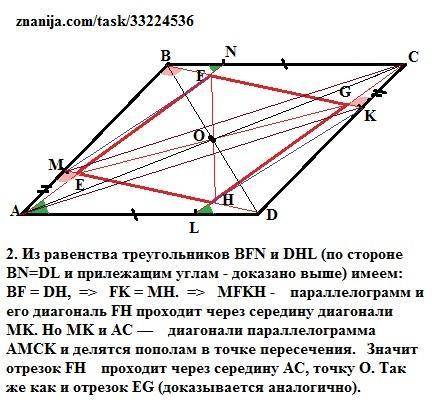
1. Треугольники АМD и CKB равны по двум сторонам и углу между ними (AD = BC - противоположные стороны параллелограмма,
AM = CK - равные части (дано) равных отрезков (АВ = CD),
∠А = ∠С - противоположные углы параллелограмма). =>
∠AMD = ∠CKB (соответственные углы равных треугольников),
∠CKB = ∠ABК (внутренние накрест лежащие углы при параллельных AВ и CD и секущей BK). => ∠AMD = ∠ABF (соответственные углы при прямых ВК и MD и секущей АВ) => BK ‖ MD.
Так же и с треугольниками ABN и СDL => AN ‖ CL.
Итак, четырехугольник EFGH - параллелограмм по признаку: противоположные стороны четырехугольника попарно параллельны.
Что и требовалось доказать.
2. Из равенства треугольников BFN и DHL (по стороне BN=DL и прилежащим углам - доказано выше) имеем: BF = DH, => FK = MH. => MFKH - параллелограмм и его диагональ FH проходит через середину диагонали MK. Но MK и AC — диагонали параллелограмма AMCK и делятся пополам в точке пересечения. Значит отрезок FH проходит через середину AC, точку О. Так же как и отрезок EG (доказывается аналогично).
Что и требовалось доказать.
Расстояние от точки до плоскости – это длина перпендикуляра, проведенного из этой точки к данной плоскости. Значит необходимо найти АВ.
Рассмотрим ∆АВМ.
ВМ=5 см по условию.
Угол АВМ=90°, так как АВ – перпендикуляр, следовательно ∆АВМ – прямоугольный.
Угол ВАМ=30° по условию.
tg(A)=BM/AB
tg(30)=5/AB
ответ: 5√3 см.