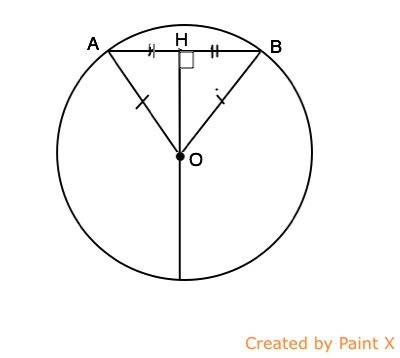
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
условие про биссектрису означает, что диагонали в точке пересечения делятся в отношении 8/6, но это означает, что основания трапеции отностятся как 8/6, то есть малое основание равно 6 (ясно, что треугольники, образованные основаниями и диагоналями, подобны).
Осталось найти высоту трапеции. К сожалению, подбор чисел подкачал. Из прямоугольного треугольника находим одну из диагоналей,
d1 = корень(8^2 - 6^2) = 2*корень(7);
d1*6 = h*8 (это просто удвоенная площадь прямоугольного треугольника), то есть
h = 3*корень(7)/2;
S = (3*корень(7)/2)*(8 + 6)/2 = 21*корень(7)/2