
ответ: 6√5 см
Объяснение:
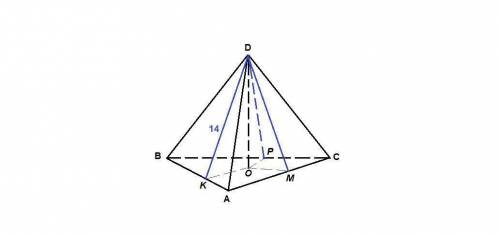
Пусть DO - высота пирамиды, DK, DM, DP - высоты боковых граней.
DK = DM = DP = 14 см по условию.
OK, OM и ОР - проекции наклонных, тогда они перпендикулярны сторонам треугольника АВС по теореме о трех перпендикулярах.
Если равны наклонные, проведенные из одной точки, то равны и их проекции, значит
ОК = ОМ = ОР, следовательно О - центр окружности, вписанной в ΔАВС, а ОК, ОМ и ОР - ее радиусы.
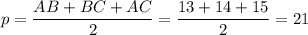
По формуле Герона
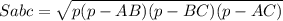
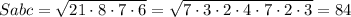 см²
см²
S = pr
84 = 21r
r = 4 см
ΔDKO: ∠DOK = 90°
по теореме Пифагора
DO = √(DK² - KO²) = √(196 - 16) = √180 = 6√5 см
Расстояние от прямой DC до плоскости α - это перпендикуляр из любой точки этой прямой на плоскость α.
Итак, в прямоугольном треугольнике АЕD катет АЕ равен по Пифагору
АЕ=√(AD²-DE²)=√(36²-18²)=18√3.
Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. То есть угол между плоскостью α и плоскостью квадрата - это угол EAD, cинус которого равен отношению противолежащего катета к гипотенузе: Sinβ=ED/AD=18/36=1/2. Значит угол между плоскостями равен 30°.
Площадь проекции квадрата на плоскость α - это площадь прямоугольника AEFB, равная S=AB*AE=36*18√3=648√3см²