Сумма острых углов прямоугольного треугольника равна 90°
=> ∠А = 90 - 45 = 45°
Так как ∠А = ∠М = 45° => ∆АВМ - равнобедренный.
=> АВ = ВМ = 22, по свойству.
ВМ - расстояние от M до АВ.
ответ: 22.
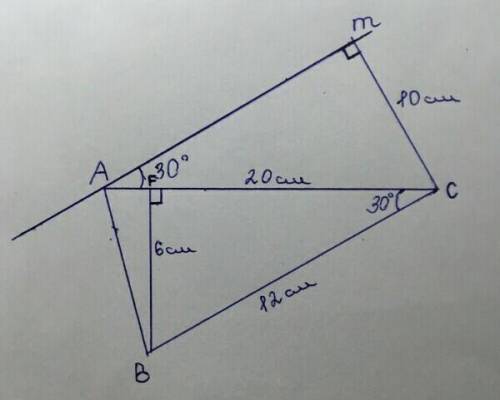
Задача #3.Решение (1 часть):
Проведём перпендикуляр BF от В до АС (он же высота)
Получился ∆BFC - прямоугольный.
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> BF = 12 ÷ 2 = 6 см.
ответ: 6 см (расстояние от В до АС).
Решение (2 часть):
При пересечении двух параллельных прямых секущей накрест лежащие углы равны.
Так как m || BC => ∠МАС = ∠С = 30°, как накрест лежащие.
Проведём перпендикуляр от m к точке С
Получился ∆МСА - прямоугольный.
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> МС = 20 ÷ 2 = 10 см.
ответ: 10 см (расстояние от прямой m до прямой ВС).
Дано:
Окружность (O;R)
ΔAOB
AB = 32 дм
OC = 12 дм
-----------------------------------
Найти:
C - ?
1. Хорда AB = 32 дм
OC = 12 дм (расстояние от центра до хорды)
AC = CB = 1/2AB = 1/2 × 32 дм = 16 дм
2. ΔOCB — прямоугольный, так как ∠BCO — прямой.
По теореме Пифагора: BO = √OC² + CB²
BO = √(12 дм)² + (16 дм)² = √144 дм² + 256 дм² = √400 дм² = 20 дм ⇒ R = BO = 20 дм
3. Воспользуемся формулой длины окружности, именно по такой формуле мы найдем длину окружности: C = 2πR
C = 2π × 20 дм = 40π дм = 40×3,14 дм = 125,6 дм
ответ: C = 125,6 дм