|BC| = a = 2√3. |2AO+2CO| = 4. |AС - (3/2)*ОС| = 3.
Объяснение:
В равностороннем треугольнике центр описанной окружности лежит на пересечении высот треугольника, которые являются и биссектрисами и медианами.
АО - радиус описанной окружности. АО=ВО=СО= R = 2 см.
1. Из формулы радиуса описанной около правильного треугольника окружности R = √3*a/3 выразим сторону треугольника: а = R√3.
Тогда |BC| = a = 2√3.
2. При сложении векторов для нахождения длины суммы векторов используется теорема косинусов.
|2AO+2CO| = 2|AO+CO| = 2*√(AO²+CO² - 2AO*CO*Cosα').
α' - угол, смежный с углом между векторами.
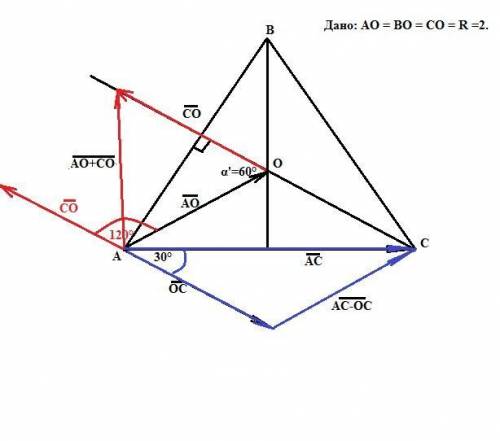
В нашем случае угол между векторами АО и СО равен 120° (при свединении начал обоих векторов в одну точку). Следовательно, при вычислении длины вектора суммы векторов АО + СО, построенного по правилу треугольника, угол α' = 60° (смотри рисунок). Тогда
|2AO+2CO| = 2*√(4+4 - 2*2*2*1/2) = 4.
3. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус угла между векторами.
Угол между векторами АС и ОС в нашем случае равен 30°(смотри рисунок). Тогда
|AС - (3/2)*ОС| = √(12+(9/4)*4 - 2*2√3*2*√3/2) = 3.
Четырехугольник можно описать вокруг окружностьи только тогда, когда суммы его противоположных сторон равны.
Пусть коэффициент отношения сторон х, тогда
первая сторона 2х,
вторая 3х
третья 7х
Периметр четырехугольника 72 см, отсюда сумма каждой пары противоположных сторон равна
72:2=36см
Сумма первой и третьей стороны равна сумме второй и четвертой.
2х=7х=9х
х=36:9=4 см
Длина первой стороны
2*4=8 см
Длина второй стороны
3*4=12см
длина третьей стороны
4*7=28 см
Длина четвертой
36-12=24 см