1
АВСD - параллелограмм
<В-<А=60 градусов
<А+<В=180 градусов => <А=180-<В
<В-(180-<В)=60
<В-180+<В=60
2×<В=60+180
2×<В=240
<В=120 гродусов
<А=180-120=60 градусов
Противоположные углы равны :
<А=<С=60 градусов ;
<В=<D=120 гродусов
ответ : 60 градусов ; 120 градусов ; 60 градусов ; 120 градусов
2
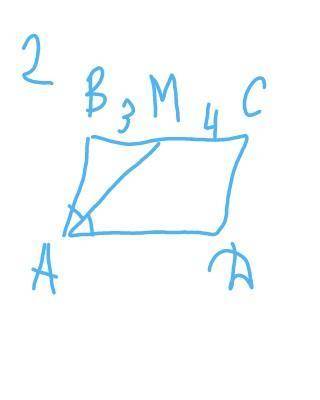
АВСD - параллелограмм
АМ - биссектриса
ВМ=3 см
МС=4 см
Биссектриса отсекает равнобедренный тр-к
АВМ :
ВМ=АВ=3 см
ВС=ВМ+МС=3+4=7 см
Р(АВСD) =2(AB+BC)=2(3+7)=20 cм
ответ : Р=20 см
3
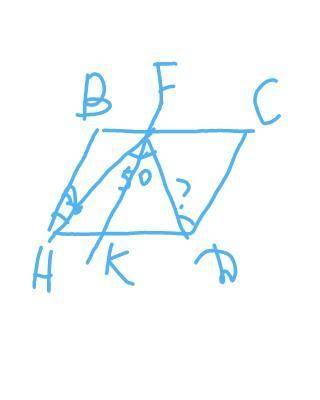
АВСD - параллелограмм
<ВАF=32 градуса
<АFD=50 градусов
<СDF=?
Проведём прямую FK параллельно АВ и СD
<AFK=<BAF=32 градуса как накрест лежащие
<КFD=<AFD-<AFK=50-32=18 градусов
<СDF=<KFD=18 градусов как накрест лежащие
ответ : <СDF=18 градусов
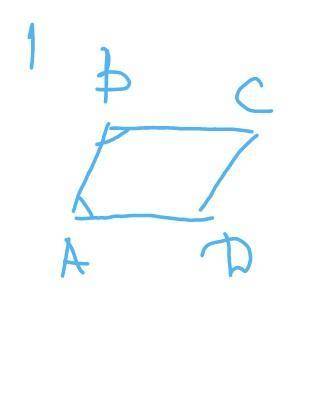
7 см
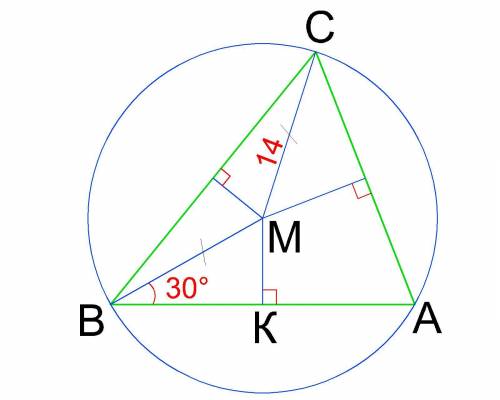
Правильное условие:
В остроугольном треугольнике ABC серединные перпендикуляры к сторонам BC и AC пересекаются в точке M. Известно, что MC = 14 см, ∠AВМ = 30°. Найдите расстояние от точки M до стороны AB. ответ дайте в сантиметрах.
Объяснение:
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке — центре описанной окружности.
Значит МА=МВ=МС=R = 14 см.
Тогда ΔАМВ - равнобедренный с основанием АВ и ∠МАВ=∠МВА=30°.
Расстоянием от т.М до стороны АВ есть высота равнобедренного ΔАМВ.
Построим высоту МК. Получили прямоугольный ΔВМК с прямым ∠МКВ и гипотенузой МВ.
Катет МК = sin∠MВK * MВ.
Т.к. ∠МВК = ∠АВМ = 30° и МА = 14 см, то
МК = sin 30° * 14 = 7 (см)
крч у равно... 2 стороны равны значит мы из 15-5,4=9,6
9.6 это две стороны-- 1 сторона = 9.6/2=4.8
Объяснение:
сделай лучшим