Задание 2
1) Все углы треугольника 180°
180° - (90° + 37°) = 180° - 127° = 53°
2) А = В так как Δ АВС - равнобедренный ( так как СD⊥ АВ)
180° - (90° + 45°) = 180° - 135° = 45°
3) По теореме "30° в прямоугольном треугольнике" АС = 2 ВС
АС = 15см значит ВС = 15 ÷ 2 = 7,5
4) По теореме "30° в прямоугольном треугольнике" СА = 2 АВ
АВ = 4 см значит СА = 4 * 2 = 8
5) АС = 8,4 см; ВС = 4,2 см значит АС = 2 ВС
По теореме "30° в прямоугольном треугольнике" ∠А = 30° и ∠С = 60° (180° - (90° + 30°) = 60°)
Задание 3 (если задача состоит в том чтобы придумать задачу то:)
Дано:
АС = 4 см
∠ВАD = 120°
Найти:
∠В - ?
АВ - ?
180° - 120° = 60° (∠ВАС)
180° - (90° + 60°) = 30°
По теореме "30° в прямоугольном треугольнике" АВ = 2 АС
АС = 4 см значит АВ = 4 * 2 = 8
ответ: ∠В = 30°, АВ = 8см
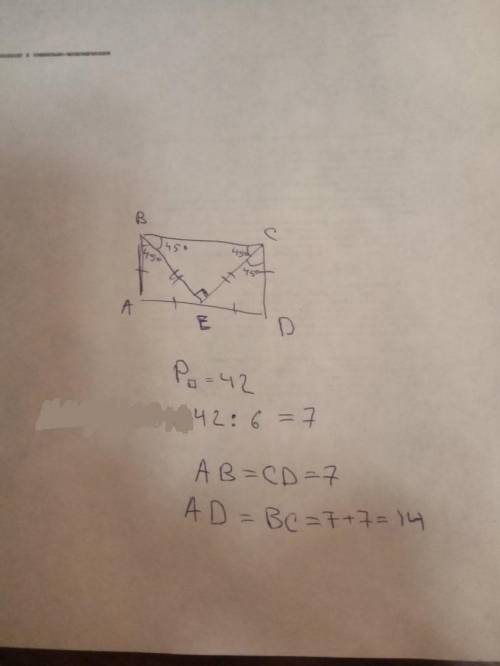
ответ: АВ=CD=7 AD=BC=14
Объяснение: назовем точку снизу как Е. треугольник ВЕС будет равнобедренным и прямоугольным, т.к. точка Е делит сторону АD пополам. Следовательно катеты треугольника будут равны и углы EBC и ECB будут равны 45 градусам. Далее следует что углы АВЕ, ECD, ВЕА и CED будут равны 45 градусам, и отсюда следует, что треугольники ABE и ECD так же равнобедренные и прямоугольные. Отсюда следует, что AB=AE=ED=CD, а сторона ВС = AD и BC = АЕ+ЕD.
Далее делим 42 на 6 = 7 (стороны АВ и CD)
а стороны AD и BC будут равны 7+7 = 14 , так как АЕ=ЕD
Пирамида SABCD. Апофема SH - высота треугольника SAB. O - точка пересечения диагоналей основания, SO - высота пирамиды.
1) Рассмотрим прямоугольный треугольник OHS. По теореме пифагора:
OH² = SH² - SO²
OH² = 4a² - 3a²
OH = a
По теореме Фалеса: BC = 2OH = 2a
Сторона основания 2a
2) SHO - линейный угол двугранного угла SABO. Найдя его, найдем и SABO, следовательно угол между боковой гранью и основанием.
Из прямоугольного треугольника SHO:
sin<SHO = SO/SH
sin<SHO = a√3/2a = √3/2
<SHO = 60°
Угол между боковой гранью и основанием 60°
3) S = Sбок + Sосн
В основании квадрат, значит Sосн = AB² = (2a)² = 4a²
Sбок = Pосн*SH/2
Pосн = 4*2a = 8a
Sбок = 8a*2a/2 = 8a²
S = 8a² + 4a² = 12a²
Площадь 12а²
4) Из точки О (это и есть центр основания) проводим перпендикуляр к апофеме SH, обозначаем H1. SH1 - расстояние от центра основания до плоскости боковой грани.
Из прямоугольного треугольника OH1H:
sin<SHO = OH1/OH
но sin<SHO = √3/2
√3/2 = OH1/a
OH1 = a√3/2
ответы: a; 60°; 12а²; a√3/2