Никак не могу как определить, каким является график функции? вот, например: y=-2/x y=2-x y=2x y=2x+2 y=2-2x y=2x-2 как понять, как выглядят эти графики? от чего это зависит? объясните подробно,
Есть несколько стандартных функций, графики и свойства которых надо запомнить:
1. Линейная функция задается уравнением y = kx + b, где k и b - некоторые числа.
Графиком является прямая.
2. Прямая пропорциональность: y = kx - частный случай линейной функции.
График тоже прямая, но обязательно проходящая через начало координат.
3. Обратная пропорциональность , где k - некоторое число.
Графиком является гипербола.
4. Квадратичная функция: y = ax² + bx + c,
График - парабола
и т.д.
Чтобы определить, как выглядит график функции, надо сравнить уравнение, которым задана функция, с уравнением в общем виде.
Например, первая функция задана уравнением, совпадающим с п. 3, где k = - 2, значит это обратная пропорциональность, графиком будет гипербола. Для его построения надо взять несколько значений х и вычислить для них соответствующие значения у, затем отметить точки на координатной плоскости и соединить.
Вторая функция y = 2 - x может быть записана иначе: y = - x + 2, теперь понятно, что уравнение совпадает с уравнением линейной функции, где k = - 1, b = 2. График - прямая. Для ее построения достаточно двух точек (значения х берем любые, у - вычисляем).
y = 2x - прямая пропорциональность, k = 2.
y = 2x + 2 - линейная, k = 2, b = 2.
y = 2 - 2x; y = - 2x + 2 - линейная, k = - 2, b = 2.
Треугольник ABC; AB=9; BC=11; BO=7. АО=ОС(медиана делит основание на 2 равные части). Чтобы найти основание, мы продолжаем медиану на 7 см и ставим точку Д(ВО=ОД=7см); соединяем со всеми вершинами и получаем ромб/параллелограм. Параллелограм состоит из 4-её треугольников, попарно одинаковых; /\АВО=/\СОД(АО=ОС, ВО=ОД и вертикальные углы при точке О); ВД=7+7=14см Воспользуемся формулой Герона: S=\/p(p-a)(p-b)(p-c), где p=(a+b+c):2 Треугольник ВСД: P=(11+9+14):2=17см S=\/17*8**6*3= \/17*4*2*3*2*3=12\/17cm^2
Отрезки пересечения этой проведенной плокости с боковыми гранями пирамиды - это средние линии треугольников, образующих боковые ребра пирамиды. Значит эти отрезки параллельны ребрам основания пирамиды. По теореме о том, что если две пересекающиеся прямые одной плоскости параллельны двум перескающимся прямым другой плоскости, то такие плосоксти параллельных, получаем требуемое утверждение. Полученный в сечении треугольник подобен треугольнику, лежащему в основании пирамиды с коэффициентом подобия 1/2. Т.е. его площадь в 4 раза меньше площади основания, т.е. равна 16.
Есть несколько стандартных функций, графики и свойства которых надо запомнить:
1. Линейная функция задается уравнением y = kx + b, где k и b - некоторые числа.
Графиком является прямая.
2. Прямая пропорциональность: y = kx - частный случай линейной функции.
График тоже прямая, но обязательно проходящая через начало координат.
3. Обратная пропорциональность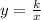
, где k - некоторое число.
Графиком является гипербола.
4. Квадратичная функция: y = ax² + bx + c,
График - парабола
и т.д.
Чтобы определить, как выглядит график функции, надо сравнить уравнение, которым задана функция, с уравнением в общем виде.
Например, первая функция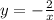
задана уравнением, совпадающим с п. 3, где k = - 2, значит это обратная пропорциональность, графиком будет гипербола. Для его построения надо взять несколько значений х и вычислить для них соответствующие значения у, затем отметить точки на координатной плоскости и соединить.
Вторая функция y = 2 - x может быть записана иначе: y = - x + 2, теперь понятно, что уравнение совпадает с уравнением линейной функции, где k = - 1, b = 2. График - прямая. Для ее построения достаточно двух точек (значения х берем любые, у - вычисляем).
y = 2x - прямая пропорциональность, k = 2.
y = 2x + 2 - линейная, k = 2, b = 2.
y = 2 - 2x; y = - 2x + 2 - линейная, k = - 2, b = 2.
y = 2x - 2 - линейная, k = 2, b = - 2.