Рисунок предлагаю только для того, чтобы убедиться, что решение выполнено верно.
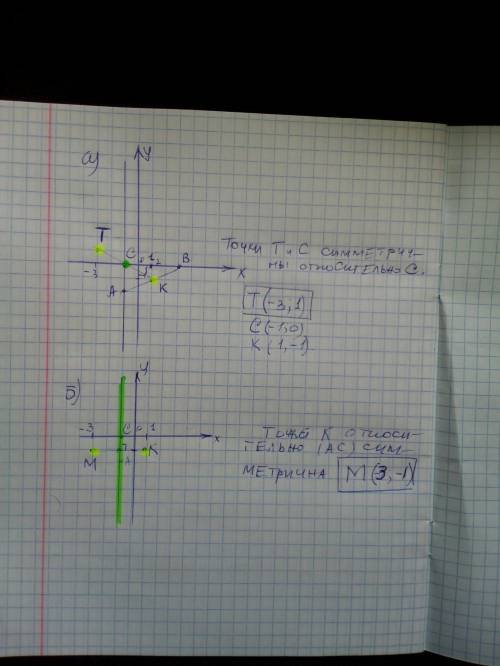
а) Найдем точку, симметричную середине отрезка АВ, относительно точки С. Пусть искомой будет точка Т(х;у), а середину АВ назовем К и найдем, сложив соответствующие координаты точек А и В, и поделив сумму на два.
(-1+3)/2=1; (-2+0)/2=-1 , К(1;-1)
Для точек Т и К точка С - середина. Значит,
(х+1)/2=-1⇒х=-2-1=-3;
(у-1)/2=0⇒у=0+1=1, т.е. искомая точка Т(-3;1)
б) Найдем теперь точку, симметричную точке К - середине АВ, относительно прямой АС, пусть это будет точка М, надо потребовать два условия: 1)точки М и К равноудалены от прямой АС 2) отрезок МК ⊥ АС, это будет точка М(-3;-1).
Т.к. искомая точка М равноудалена от прямой АС, АС параллельна оси оу, уравнение прямой АС имеет вид х=-1, значит, зная абсциссу середины отрезка КМ, и абсциссу точки К, находим абсциссу точки М из условия (х+1)/2=-1; откуда х=-2-1=-3, ордината совпадает с ординатой точки К и ординатой середины отрезка М, т.к. МК и АС перпендикулярны. а АС параллельно оси оу.
Рисунки во вложении.
1) 180-50-35= 95
2) Воспользуемся тем, что сумма всех внутренних улов всякого треугольника всегда составляет 180°, а также тем, что у всякого равнобедренного треугольника углы при основании одинаковы.
Обозначим через x величину одного из улов при основании в данном равнобедренном треугольнике.
Тогда величина другого угла при основании этого треугольника также будет равна х.
Так как величина угла при вершине составляет 80°, можем составить следующее уравнение:
х + х + 80 = 180,
решая которое, получаем:
2х + 80 = 180;
(2х + 80) / 2 = 180 / 2;
х + 40 = 90;
х = 90 - 40;
х = 50°.
ответ: 50°
3) Дано:треугольник АВС - равнобедренный;
угол ВСА = углу ВСА = угол АВС + 36;
Найти углы: ВСА, ВСА, АВС
Решение: Пусть угол АВС - х градусов, тогда угол ВСА = углу ВСА = угол х + 36 градусов. Нам известно, что сумма градусных мер любого треугольника 180 градусов. Составляем уравнение:
х + 36 + х + 36 + х = 180;
3 * х = 180 - 72;
х = 108 : 3;
х = 36 градусов - угол АВС.
36 + 36 = 72 градуса - угол ВСА = углу ВСА.
ответ: 36 градусов, 72 градуса и 72 градуса.
4)
Дано: прямоугольный треугольник, углы обозначим 1, 2, 3; пусть угол 3 - прямой (90о), а угол 1 больше угла 2 на 20о.
Найти: величину угла 1 и величину угла 2.
Решение: Сумма углов в треугольнике равна 180о. 1 + 2 + 3 = 180о; 1 + 2 = 180о - 90о = 90о; предположим, что углы равны 1 = 2, тогда 1 + 2 = 90о + 20о = 110о, а значит угол 1 = 110о : 2 = 55о, а угол 2 = 90о - 55 = 35о.
ответ: один угол 55о, а второй угол 35о.
5) Для решения данной задачи, вспомним условие существования треугольников. У треугольника сумма любых двух сторон должна быть больше третьей.
1) Проверим существование треугольника со сторонами 5 см, 3 см, 8 см.
5<3+8; 5<11.
3<5+8; 3<13.
8= 5+3; 8=8 .
Так как сторона в 8 сантиметров равна сумме двух других, то данного треугольника не существует.
ответ: не может.
Повышенный уровень:
1)) Биссектриса делит угол А на 2 угла а, а угол В на 2 угла b. Имеем
2 а + 2b + 110 = 180. Или а + b = 35.
Но из треугольника АОС имеем а+b+Х = 180. Х = 180 - 35 = 145.
2) Начнём с того, что катет, лежащий против угла 30 равен половине гипотенузы.
Третий угол треугольника равен 180 — (90 + 60) = 30
Против 30 всегда лежит меньший катет.
Если Х — это меньший катет, то гипотенуза 2Х
Если сумма катета и гипотенузы равна 18, то Х + 2Х = 18
3Х = 18
Х = 18/3 = 6 см
6 см — это катет
6 * 2 = 12 см — это гипотенуза
ответ: 12 см, 30 градусов