Сумма углов треугольника 180°. =>
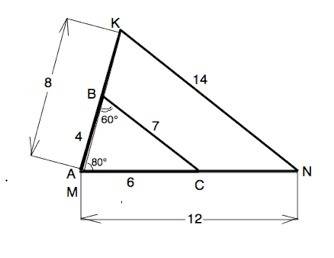
В ∆ АВС угол С=180°-(80°+60°)=40°
Сравним стороны данных треугольников, начиная с меньшей.
АВ=4, МК=8
АС=6, МN=12
BC=7, KN=14
Отношение длин сторон этих треугольников 1:2.
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Против сходственных сторон лежат равные углы.
Угол М заключён между МK и МN, т.е. между сторонами, пропорциональными АВ и АС меньшего треугольника и лежит против КN. =>
угол М=углу А=80°
Угол К лежит против МN и заключен между КМ и КN, эти стороны пропорциональны ВА и ВС соответственно.
Угол К=углу В=60°
Угол N=углу С=40°
Решение
MK - средняя линия тр-ка ABD и по теореме о средней линии
MK || AD
аналогично
МР|| АС
Теорема ( признак параллельности плоскостей)
Если две пересекающие прямые МК и МР одной плоскости, соответственно параллельны двум пересекающимся прямым AD и АС другой плоскости, то эти плоскости параллельны, то есть
(MKP) || (ACD)