
18 см
Объяснение:
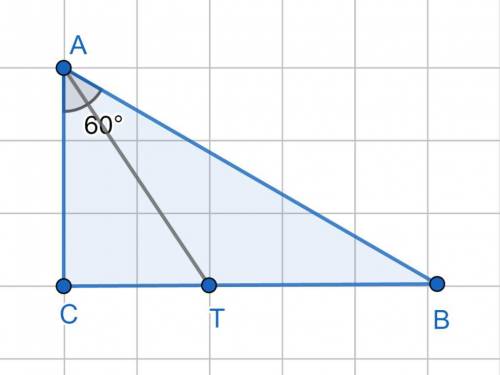
1) Т.к. <C = 90°, <BAC = 60°, то <ABC = 90° - 60° = 30°
2) AT - биссектриса, следовательно по определению она делит угол BAC пополам, а значит <CAT = <BAT = 60° : 2 = 30°.
3)Получаем, что в треугольнике ATB два угла равны 30°, следовательно этот треугольник равнобедренный, т.е. AT = TB = 12 см.
4) Рассмотрим ΔACT: он прямоугольный, <CAT = 30°. Катет лежащий напротив угла 30° равен половине гипотенузы, т.е. CT = AT : 2 = 12 : 2 = 6 (см)
5) CB = CT + TB = 6 + 12 = 18 (см)
Решение.
1)MN-касат.
OE-r-следовательно <MEK=90º=>KE-высота, медиана, биссектриса.
КЕ-медиана=>МЕ=ЕN=20:2=10
2)OD-r
MK-касат=><KDO=90º
3)Рассмотрим треу. MEK и DOK.
<MEK-общий, <KDO=<MEK=>треу. MEK ~ DOK.(по двум углам)
4)MN и MK-касат.,MD-10=>ME=MD (по двум касат.)
DK=MK-MD=26-10=16см.
5) треу. MKE-прямоуг.
MK^2=ME^2+EK^2(теорема Пифагора. )
EK=корень ME^2-MK^2=корень из 676-100=корень из 576=24.
6)Отношение.
10/OD=24/16=26/OK
24/16=26/OK
24×OK=16×26
24OK=416
OK=416:21
OK=17целых1/3
OE=EK-OK=24-17целых1/3=6целых2/3 (а не 6и1/3, как было в ответе).
Можно было решить так:
По формуле радиуса вписанной в треугольник окружности:
r=S/p, где S - площадь, а "р" - полупериметр треугольника.
У нас р=(26+26+20):2 = 36.
S=√[p(p-a)((p-b)(p-c)] - формула Герона.
S=√(36*18*18*16)=240.
r=240/36=6и2/3.
ответ: r=6и2/3.