Объяснение:
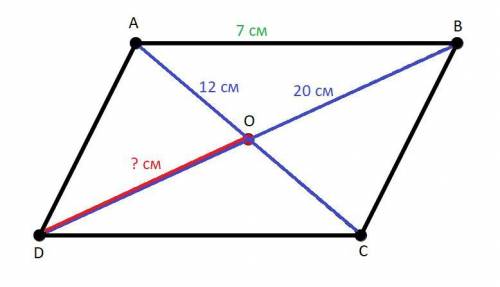
Дано:
ABCD - параллелограмм.
AC и BD - диагонали параллелограмма.
AC ∩ BD = O.
AC = 12 (см); BD = 20 (см); AB = 7 (см).
Найти:
DO - ? (см).
Тут всё довольно просто. Так как ABCD - параллелограмм, вспомним свойство такой геометрической фигуры: диагонали параллелограмма точкой пересечения делятся пополам. Т.е. диагонали AC и BD делятся точкой пересечения O пополам. Соответственно DO будет равняться половине всей диагонали BD. (и из этого следует, что DO = OB)
DO = BD/2 = 20 : 2 = 10 (см)
1. угол ВОА=СОD как вертикальные
треугольник АОВ=DOC по двум углам и стороне между ними (AO=DO, угол А=D, угол ВОА=СОD)
2 признак равенства треугольников
2. проводим отрезок АС
треугольник АСВ=АСD, т к две стороны равны по условию и АС - общая (3 признак)
из равенства треугольников следует равенство их соответственных элементов
=> угол В=D