ответ: измерени паралелипипеда 4,2,3=
Объяснение:
439°
Даны вершины: A,(-3, 3) B (7, 5)C (4, 1).
Угол между прямыми АВ и АС можно определить двумя
1) геометрическим по теореме косинусов,
2) векторным через скалярное произведение.
1) Расчет длин сторон
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √104 ≈ 10,19804.
BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √25 = 5.
AC (в) = √((Хc-Хa)²+(Ус-Уa)²) = √53 ≈ 7,28011.
cos A= АВ²+АС²-ВС² = 0,88897.
2*АВ*АС
A = 0,475695219 радиан,
A = 27,25532837 градусов .
2) х у Длина
Вектор АВ 10 2 10,19804.
Вектор АС 7 -2 7,28011.
Угол определяем по формуле:
α = arc cos |ax*bx+ay*by|/(√(ax^2+ay^2)*√(bx^2+bу^2)).
α = arc cos |10*7+2*(-2)|/(√104*√53) = 66/2√1378 = 33/√1378 ≈
33/37,12142239 ≈ 0,88897.
Угол дан выше.
.
12 корней из 6
Объяснение:
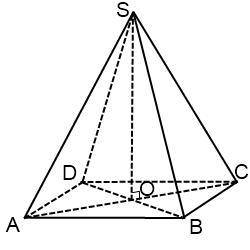
S= 2a*h
a=AB h=SO
Найдем их.
P=4a => a=P/4=24/4=6
d- диагональ квадрата
d=a корней из 2 (можно получить по теореме Пифагора для прямоугольного треугольника ABC со сторонами а и гипотенузой d).
Тогда АО = d/2= a корней из 2 /2=3 корня из 2
Рассмотрим треугольник AOS. Он прямоугольный с углом SA0=30 градусов.
SA=SO/sin 30 => SA=2SO
Обозначив высоту SO=x, по теореме Пифагора имеем:
(2x)^2 - x^2= (3 корня из 2)^2
3x^2= (3 корня из 2)^2
3x^2=18
x^2=6
x=корень из 6 =h
S= 2a*h= 2*6*корень из 6= 12 корней из 6
го 67+372 шшгнноорнвгвш