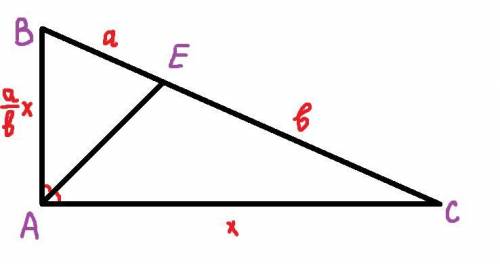
Пусть дан треугольник АВС с прямым углом А, в котором проведена биссектриса АЕ, длину которой нужно найти.
Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.
Запишем пропорцию:
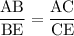
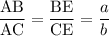
Пусть 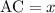 . Тогда
. Тогда 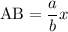 .
.
Запишем теорему Пифагора для треугольника АВС:
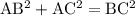
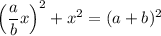
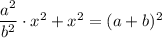
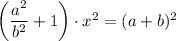
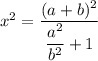
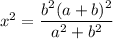
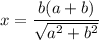
Значит:
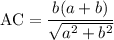
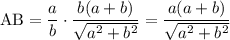
Запишем теорему синусов для треугольника АЕС:
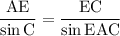
Так как АЕ - биссектриса, то ЕАВ и ЕАС равны по половине прямого угла, то есть по 45°.
Синус угла С определим как отношение противолежащего катета к гипотенузе:
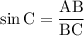
Теперь можем найти биссектрису:
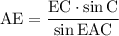
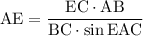
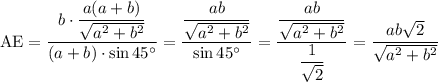
ответ: 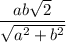
5х=150
х=150/5
х=30
∠К=30°, ∠L = 60°, ∠M=90° ⇒ KL - большая сторона.
2. ∠DEC=180-120 = 60°
sin∠DEC= DC/ DE
√3/2 = 5/DE
DE=5/(√3/2) = 10/√3
3. Вопрос: как указана точка N? Отрезки будут равны, если являются радиусами окружности с центром в т. N, а стороны треугольника являются касательными к этой окружности (перпендикуляра проведены в точки касания). В другом случае, эти перпендикуляры отсекают подобные треугольники (по двум углам), но не равные.