а)
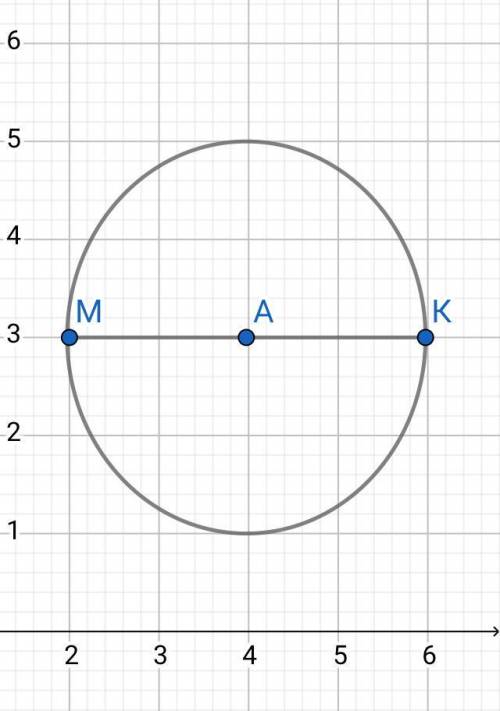
Пусть A - центр окружности.
А(х) = M(x) + K(x)/2 = 2 + 6/2 = 4
A(y) = M(y) + K(y)/2 = 3 + 3/2 = 3
Итак, координаты точки А (4;3).
б)
АК и АМ - радиусы окружности.
АМ = √((M(x) - A(x))² + (M(y) - A(y))²) = √((2 - 4)² + (3 - 3)²) = √4 = 2 ед.
Т.е. радиус данной окружности = 2 ед.
в)
Уравнение окружности: (х - х₀)² + (у - у₀)² = R², где (х₀;у₀) - координаты центра окружности; (х;у) - координаты точки на окружности; R - радиус окружности.
Уравнение данной окружности: (х - 4)² + (у - 3)² = 4
г)
Данная окружность на рисунке.
М ... Ну тут просто нужно вспомнить, что tg - отношение противолежащего катета к прилежащему. Стало быть, BC/AC = 2/3.
cos - отношение прилежащего катета к гипотенузе, т. е. AC/AB = 3/5. Т. е. можно взять, например, BC = 2 см, AC = 3 см ... и т. д. Единицы измерения выбери по вкусу = )