Объяснение:
рис. во вложении
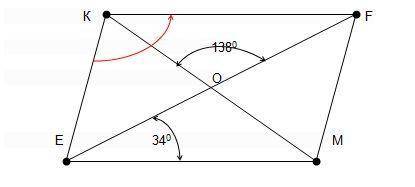
Диагонали параллелограмма, в точке их пересечения делятся пополам, значит ОК = ОМ = КМ / 2.
По условию, КМ = 2 * FM, отсюда ОМ = FM.
Треугольник ОМF равнобедренный. Угол FOM и FOK смежные углы, значит угол FOM = 180 – 138 = 42°.
Так как треугольник OMF равнобедренный, то угол FOM = OFM = 42°. В треугольнике EFM определим угол EMF.
Угол EMF = 180 – FEM – EFM = 180 – 34 – 42 = 104°. Так как у параллелограмма противоположные углы равны, то угол ЕКF = EMF = 104°.
Угол ЕКF равен 104°.
При решении подобных задач нужно помнить о неравенстве треугольника. В теореме о неравенстве треугольника утверждается, что в треугольнике любая сторона меньше суммы двух других.
Можно рассматривать два случая:
1) большей стороной является основание;
2) большей является боковая сторона.
Если принять боковую сторону равной х, то для равнобедренного треугольника по этому условию получим х+х < 3х. Поэтому основание не может быть большей стороной, т.к. не удовлетворяет неравенству треугольника.
( Боковые стороны тогда просто не "дотянутся" друг до друга и "улягутся" на основание).
-------------------------
Примем основание треугольника равным х. Тогда боковые стороны равны 3х каждая.
Р= х+3х+3х=7х
7х=50