10√2
Объяснение:
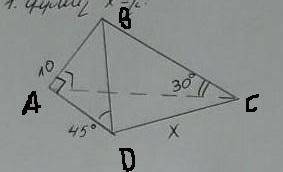
<BAD=90, а <ADB=45 по условию, значит <ABD=180-90-45=45, а значит △ABD - прямоугольный равнобедренный. Значит AB=AD=10.
Также по условию <BAC=<ADB=45, значит <CAD=<CAB=45. Рассмотрим тр-ки △ABC и △ADC. У них AC - общая, AB=AD, <CAD=<CAB, значит они равны по 1му признаку. =>BC=DC=x, <ACB=<ACD=30, значит △CBD - равнобедренный, а его <BCD=60. Но тогда 2 оставшихся угла тоже равны 60, а △CBD на самом деле равносторонний, и BC=DC=BD.
Найдём в △ABD гипотенузу BD:
BD²=AD²+AB²=10²+10²=200
x=BD=10√2
Даны вершины: A,(-3, 3) B (7, 5)C (4, 1).
Угол между прямыми АВ и АС можно определить двумя
1) геометрическим по теореме косинусов,
2) векторным через скалярное произведение.
1) Расчет длин сторон
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √104 ≈ 10,19804.
BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √25 = 5.
AC (в) = √((Хc-Хa)²+(Ус-Уa)²) = √53 ≈ 7,28011.
cos A= АВ²+АС²-ВС² = 0,88897.
2*АВ*АС
A = 0,475695219 радиан,
A = 27,25532837 градусов .
2) х у Длина
Вектор АВ 10 2 10,19804.
Вектор АС 7 -2 7,28011.
Угол определяем по формуле:
α = arc cos |ax*bx+ay*by|/(√(ax^2+ay^2)*√(bx^2+bу^2)).
α = arc cos |10*7+2*(-2)|/(√104*√53) = 66/2√1378 = 33/√1378 ≈
33/37,12142239 ≈ 0,88897.
Угол дан выше.
.
↓
Объяснение:
1. x²−2⋅x+y²+z²−4⋅z−4=0.
(x−1)²+y²+(z-2)²=9
О (1;0;2) радиус 3
2. O(1;3;2) B(1;0;−2),
R=OB=√(0+9+16)=5
(x-1)²+(y-3)²+(z-2)²=25