Дано :
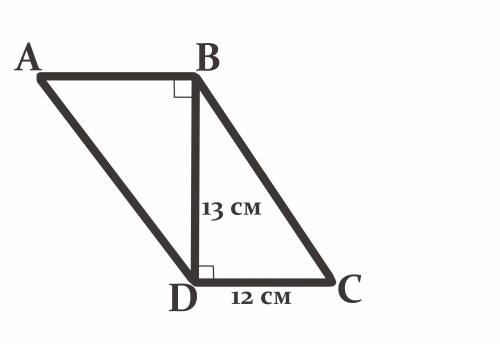
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
Sп.п.= S бок+2S осн.
S осн.ABCD =1/2*10*24=120 кв.см.
S бок =h*Pосн.
H=tg45*10(DB1)
P=A1B1+B1C1+C1D1+D1A1
Т.к. диагонали пересекаются под прямым углом и делятся точкой пересечения пополам, то из прямоуг. треуг. A1OD1 с катетами 5 и 12 см. находим сторону ромба. √25+144=13 см.
P(A1D1B1C1) =4*13=52см.
Sбок=52*10=520кв.см.
S полн=2*120+520=760кв.см.