Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника.
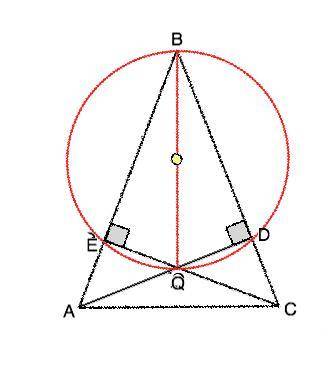
В четырехугольнике BEQD проведем диагональ ВQ, которая является общей гипотенузой треугольников DEQ и BDQ. Радиус окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы и равен её половине. Следовательно ,для прямоугольных треугольников ВEQ и BDQ описанная окружность будет общей и описанной около четырехугольника BEQD. Доказано.
* * *
Решение этой задачи может опираться на теорему о четырехугольнике, около которого описана окружность. Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность. Два противоположных угла прямые, их сумма 180°, следовательно, сумма ∠В+∠Q=180° ⇒ около четырехугольника BEQD можно описать окружность.
Вторая задача: Прямая ВС лежит в плоскости (АВС), так как 2 её точки В и С лежат в плоскости (АВС). Прямая АМ пересекает плоскость (АВС) в точке А, не лежащей на ВС, значит АМ и ВС скрещивающиеся прямые.
Третья задача: PK средняя линия треугольника АВС, поэтому равна 1/2 ВС=8:2=4Доказательство. МН средняя линия треугольника DBC (по условию), значит МН || BC и с плоскостью МНК. не имеет общих точек, поэтому РК тоже не может иметь с ВС общих точек, но РК и ВС лежат в одной плоскости треугольника АВС, значит РК и ВС параллельны. Так, как к середина АС, то и Р должна быть серединой АВ.
Этого хватит, ты мало выставил, так бы все решил. Удачи!!