r = 6 см
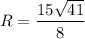 см
см
Объяснение:
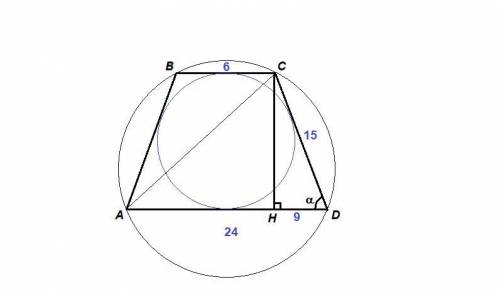
Трапеция вписана в окружность, значит она равнобедренная.
AB = CD.
Трапеция описана около окружности, значит суммы противоположных сторон равны.
AB + CD = AD + BC = 24 + 6 = 30 см
AB = CD = 30 : 2 = 15 см
Проведем высоту СН.
По свойству равнобедренной трапеции отрезок HD равен полуразности оснований:
HD = 0,5 · (AD - BC) = 0,5 · (24 - 6) = 0,5 · 18 = 9 см
ΔCHD: ∠CHD = 90°, по теореме Пифагора
CH = √(CD² - HD²) = √(15² - 9²) = √(225 - 81) = √144 = 12 см
Радиус окружности, вписанной в трапецию, равен половине ее высоты.r = 0,5 CH = 0,5 · 12 = 6 см
ΔCHD: ∠CHD = 90°
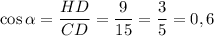
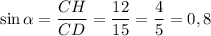
Из ΔACD по теореме косинусов:
AC² = AD² + CD² - 2 · AD · CD · cosα
AC² = 24² + 15² - 2 · 24 · 15 · 0,6
AC² = 576 + 225 - 432 = 369
AC = √369 = 3√41 см
Треугольник ACD вписан в ту же окружность, что и трапеция.
По следствию из теоремы синусов:

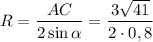
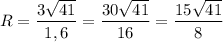 см
см
1) 18см
2) 12см
3) 6см
4) 27см.
Найдите стороны четырехугольника.
Объяснение:
Пусть длина 1 стороны - х см.
Запишем % в десятичном виде:
50%=50/100=0,5
150%=150/100=1,5
1 сторона - х см
2 сторона - 2/3х
3 сторона - (2/3х)×0,5
4 сторона - 1,5х
Р (периметр) - 63 см
1)Составим уравнение:
х+2/3х+(2/3х)×0,5+1,5х=63
х+2/3х+(2/3)×(1/2)х+3/2х=63
х+2/3х+1/3х+3/2х=63 | ×6
6х+4х+2х+9х=63×6
21х=378
х=378:21
х=18 см первая сторона;
2) 18×2/3=12 (см) вторая сторона;
3) 12×0,5=6 (см) третья сторона;
4) 18×1,5=27 (см) четвертая чторона.
1 сторона 18 см
2 сторона 12 см
3 сторона 6 см
4 сторона 27 см.
ответ:8+2•10=28 см периметр
Объяснение: