1) 2+7=9
360°:9=20° в одной части.
Значит дуга АМС имеет градусную меру 40°
Угол АОС - центральный угол, измеряется дугой на которую он опирается.
∠АОС=40° ⇒∠АВС=140° ( сумма углов четырехугольника равна 360° и углы ВАО и ВСО - прямые)
Отрезки касательных, проведенных к окружности из одной точки равны, АВ=ВС
Треугольник АВС равнобедренный с углом 140° при вершине, значит углы при основании (180°-140°):2=20°
О т в е т. 20°; 140°; 20°
2) 4+5=9
360°:9=20° в одной части.
Значит дуга АМС имеет градусную меру 80°
Угол АОС - центральный угол, измеряется дугой на которую он опирается.
∠АОС=80° ⇒∠АВС=100° ( сумма углов четырехугольника равна 360° и углы ВАО и ВСО - прямые)
Отрезки касательных, проведенных к окружности из одной точки равны, АВ=ВС
Треугольник АВС равнобедренный с углом 100° при вершине, значит углы при основании (180°-100°):2=40°
О т в е т. 40°; 100°; 40°
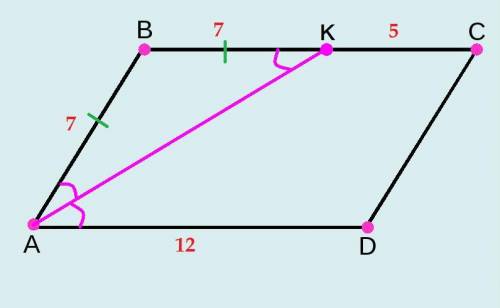
Противолежащие стороны параллелограмма равны (из свойства фигуры параллелограмм).
=> BC=AD=12 (см) => BK=12-5=7 (см).
Так как АК - биссектриса (по условию), то она делит угол А так, что углы ВАК и КАD равны между собой.
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны (из определения).
=> при пересечении двух параллельных прямых секущей накрест лежащие углы равны.
=> угол ВКА = углу КАD, а они накрест лежащие при ВС || АD и секущей АК.
В равнобедренном треугольнике две боковые стороны равны и углы при основании тоже равны (из свойства равнобедренного треугольника).
=> треугольник АВК - равнобедренный (угол ВАК = углу ВКА) и АВ=ВК=7 (см).
Периметр параллелограмма равен удвоенной сумме 2х его соседних сторон (из теоремы о периметре параллелограмма).
=> Р=2*AB+2*AD=2*7+2*12=14+24=38 (см).
ответ: Р параллелограмма АВСD равен 38 (см).
все элементы подобных многоугольников(сторона,высота, периметр) имеют отношение k - коэффициент
k = P1 : P2 = 5 : 7
площади многоугольников имеют отношение k^2 = S1 : S2
тогда
S1 / S2 = (5/7 )^2 < отсюда S1=S2*(5/7 )^2
S1+S2 = 296
подставим S1
S2*(5/7 )^2 +S2 =296
S2 *( (5/7 )^2 + 1) = 296
S2 = 296 / ( (5/7 )^2 + 1) =296 / (74/49 ) = 296*49 / 74 =196 см2
S1 =296 -196 =100 см2
ответ 100 см2 ; 196 см2