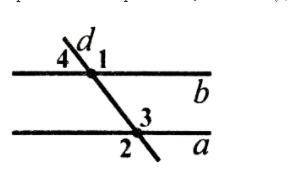
1.
Обозначим радиус меньшей окружности буквой r, а большей - R.
По условиям задачи r/R=2/7.
Ширина полосы будет равна R-r и по условиям равна 24 (см), значит: R-r=24 (см), то есть R=r+24 (см).
С учетом полученного результата имеем:
r/r+24=2/7,
7r=2*(r+24),
7r=2r+48,
5r=48,
r=9,6 (см).
Так как R=r+24, то R=9,6+24=33,6(см).
Таким образом диаметр одной окружности будет равен D=2R=33,6*2=67,2(cм), а диаметр второй окружности будет равен
d=2r=9,6*2=19,2 (см).
2.
Расстояние между центрами окружностей - отрезок ОА делится точкой ка в отношении 2:3. Значит, отрезок ОА разделен на 2+3=5 равных частей. Причем ОК содержит 2 части, а КА - 3 части.
10 см : 5 = 2 см - длина каждой из равны частей.
Тогда ОК=2*2 = 4 см. Диаметр меньшей окружности равен 2*4=8 см.
АК = 3*2 = 6 см. Диаметр большей окружности равен 2*6 = 12 см.
Наверное вот так ...
A1. Две прямые на плоскости называются параллельными, если они:
4) не пересекаются
А2. Один из признаков параллельности двух прямых гласит:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А3. Выберите утверждение, являющееся аксиомой параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
А4. Если две параллельные прямые пересечены секущей, то:
Соответственные углы равны
А5. Если прямая перпендикулярна одной из двух параллельных прямых, то:
Она перпендикулярна и другой
А6. Всякая теорема состоит из нескольких частей:
Условия и заключения
А7. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:
Накрест лежащие, соответственные, односторонние
А8. Аксиома – это:
Положение геометрии, не требующее доказательства
А9. Выберите утверждение, которое является признаком параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А10. Если прямая не пересекает одну из двух параллельных прямых, то:
Другую прямую она тоже не пересекает
или
С другой прямой она совпадает
Угол 3 = 120°
Угол 4 = 60°
Объяснение:
1) Углы 1 и 2 внутренние разносторонние при сечной d, а значит они равны, тоесть угол 1 = углу 2 = 240°/2 = 120°. Так как углы 1 и 4 смежные, угол 4 = 180° - 120° = 60°, а углы 3 и 2 вертикальные, так что они равны.