Чертежи к задаче - во вложении.
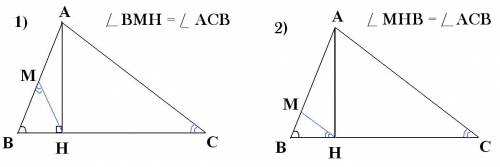
По условию задачи в силу подобия треугольников АВС и ВМН необходимо рассмотреть 2 случая.
1-й случай.
Из подобия треугольников следует равенство ∠АВС=∠MBH (по условию) и ∠АСВ=∠ВMН.
Тогда отношение сходственных сторон:
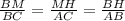
По теореме косинусов в ∆АВС АС²=АВ²+ВС²-2·АВ·ВС·cos B=18²+16²-2·18·16·4/9=18²+16²-16²=18² => AC=18
В прямоугольном ∆АНВ ВН=АВcosB= 18·4/9=8
Тогда получим
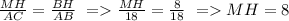
2-й случай.
Из подобия треугольников следует равенство ∠АВС=∠MBH (по условию) и ∠АСВ=∠MНB.
Тогда MH||AC и отношение сходственных сторон:
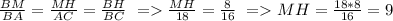
ответ: 8 или 9.
Если ВВ1 - хорда, а С -её середина, то прямоугольный треугольник ОСВ (и равный ему треугольник ОСВ1) - с катетом ВС= 30/2 = 15 и гипотенузой OB = 17, поэтому второй катет СО = 8; (Пифагорова тройка 8,15,17).
Треугольник АВC - прямоугольный и подобный треугольнику ОВС - у них равные острые углы - например, угол ВАС равен углу СВО, потому что у этих углов стороны попарно перпендикулярны.
Поэтому АС/ВС = ВС/СО;
AC = 15^2/8 = 225/8;
Для любителей формул можно заметить, что ВС - высота к гипотенузе АО в прямоугольном треугольнике АВО, и она делит гипотенузу на отрезки АС и СО.
Поэтому ВС^2 = AC*CO
Я просто предпочитаю не пользоваться формулами - всегда есть риск применить готовое соотношение не там, где надо.
ответ в прикрепленной фотографии