Два треугольника равны по третьему признаку равенства треугольников, если ...
Выберите один из 3 вариантов ответа:
1) две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника ;
2) сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника ;
3) три стороны одного треугольника соответственно равны трём сторонам другого треугольника.
ответ: 3).Задание №2.Дано:ΔABD и ΔCBD;
AB = BC;
AD = DC.
Доказать:ΔABD = ΔCBD
Доказательство:1. AB = BC (по условию) |
2. AD = DC (по условию |⇒ ΔABD = ΔCBD (по третьему признаку).
3. BD - общая сторона |
Что и требовалось доказать!
ответ: 2).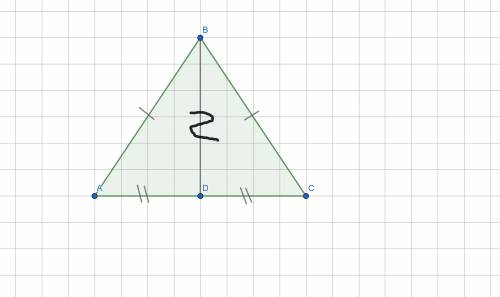
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
Верно. Аксиома планиметрии 9: через точку, не лежащую на данной прямой можно провести на плоскости не более одной прямой, параллельной данной.
2) Треугольник со сторонами 1,2,4 существует
Неверно. Длина каждой стороны треугольника не может быть больше или равна сумме двух других. 4>1+2 (неравенство треугольника)
3) Если в ромбе один из углов равен 90 гр, то такой ромб - квадрат
Верно. Сумма углов четырехугольника 360°. Ромб - параллелограмм, все стороны которого равны. Противоположные углы ромба равны. Если один угол равен 90°, противоположный равен 90°. Два других равны 90°. Квадрат - параллелограмм, все стороны которого равны (ромб) и все углы прямые (прямоугольник).