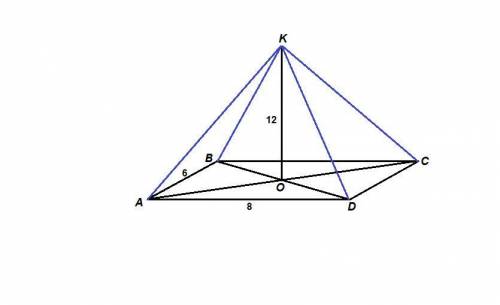
KA = KB = KC = KD = 13
Объяснение:
Из прямоугольного треугольника АВС находим АС по теореме Пифагора:
АС = √(АВ² + ВС²) = √(36 + 64) = 10
Диагонали прямоугольника равны и точкой пересечения делятся пополам:
АО = ВО = СО = DO = 5
АО, ВО, СО и DO - проекции наклонных KA, KB, KC и KD на плоскость прямоугольника.
Если равны проекции наклонных, проведенных из одной точки, то равны и сами наклонные, т.е.
KA = KB = KC = KD.
Из прямоугольного треугольника АОК по теореме Пифагора находим КА:
КА = √(ОК² + АО²) = √(12² + 5²) = √(144 + 25) = √169 = 13
KA = KB = KC = KD = 13
Объяснение:
Пусть АВ, АС будут боковыми сторонами треугольника, тогда сторона ВС будет основанием.
Дано:
∆АВС - равнобедренный
Рabc = 13 см (периметр)
ВС = 3 см (основание)
АВ, АС = ?
Мы знаем, что у равнобедренного треугольника боковые стороны равны. ∆АВС - равнобедренный => АВ = АС. Если Рabc = 13 см и ВС = 3 см, тогда:
АВ = АС = (Рabc - BC) / 2 = (13 - 3) / 2 = 10 / 2 = 5 см.