В трапеции ABCD биссектриса угла BAD проходит через точку М, которая является серединой CD. Известно, что АВ=5, АМ=4. Найдите длину отрезка ВМ.
По условию СМ=CD.
Решить задачу можно разными
Проведем МК || AD - по т. Фалеса она делит АВ в отношении DM:MC т.е. на АК=КВ.
В ∆ АКМ ∠КМА= ∠МАD - как накрестлежащие.
∠МАD=∠МАК- как половины ∠КАD
∠КАМ=∠КМА⇒
∆ АКМ - равнобедренный, и АК=КМ.
Но КМ=АК=КВ ⇒ ∆ ВКМ равнобедренный, ⇒ ∠КВМ=∠КМВ.
Углу КМВ равен накрестлежащий ∠ СВМ. ⇒ ВМ - биссектриса угла СВК.
В трапеции сумма углов, прилежащих к одной боковой стороне, равна 180º
Тогда сумма их половин равна 90º, и угол ВМА=180º-90º=90º
∆ АВМ - прямоугольный. Отношение катета АМ к гипотенузе АВ 3:5⇒ ∆ АВМ - египетский, и ВМ=3 (ед. длины) ( по т.Пифагора получим ту же величину).
Доказав, что ∆ АКМ - равнобедренный, проведем в нем высоту КН. Она же - медиана, и АН=НМ.
Тогда КН - средняя линия ∆ АВМ, и КН || ВМ, откуда следует, что угол ВМА=90º, ∆ АВМ - египетский и ВМ=3 (ед. длины).
на любителей т. косинусов)
По т. косинусов можно из ∆ КАМ найти косинус угла КАМ, затем по ней той же теореме длину ВМ.
Вычисления приводить не буду - пользовалась при нахождении косинуса инженерным калькулятором. Без него значения будут лишь приближенными. Таким образом найден
cos ∠КАМ=0,8.
Тогда ВМ²=5²+4²-2•5•4•0,8 ⇒
BM²=25+16-32=9
BM=3 (ед. длины)

russian.
тригонометрические функции острого угла в прямоугольном треугольнике. sin, cos, tg, ctg
итак, у каждого прямоугольного треугольника есть два острых угла. для каждого из них можно найти синус, косинус, тангенс и котангенс. здесь главное не перепутать, что к чему относится.
синус острого угла пр. треугольника - это отношение (деление) противолежащего этому углу катета к гипотенузе.
косинус острого угла пр. треугольника - это отношение (деление) прилегающего к этому углу катета к гипотенузе.
тангенс острого угла пр. треугольника - это отношение противолежащего этому углу катета к прилегающему катету.
котангенс - это наоборот, отношение прилегающего к этому углу катета к противолежащему.
во вложении есть рисунок, там все показано. легче это понять словами, а не на рисунке (лично для меня).
также существует таблица значений синуса, косинуса, тангенса и котангенса для некоторых углов (30°, 45°, 60°, 90°), тоже во вложении. таблицу нужно выучить обязательно.
ukrainian.
тригонометричні функції гострого кута прямокутного трикутника. sin, cos, tg, ctg.
у кожному прямокутному трикутнику є два гострих кута. для кожного з них можна знайти синус, косинус, тангенс та котангенс.
синус гострого кута пр. трикутника - це відношення (ділення) протилежного цьому куту катета до гіпотенузи.
косинус гострого кута пр. трикутника - це, відношення прилеглого цьому куту катета до гіпотенузи.
тангенс гострого кута пр. трикутника - це відношення протилежного цьому куту катета до прилеглого.
котангенс - це, навпаки, відношення прилеглого до цього кута катета до протилежного.
також існує таблиця значень синуса(sin), косинуса (cos), тангенса(tg) та котангенса (ctg) для деяких кутів (30°, 45°, 60°, 90°). таблицю потрібно вивчити.
таблицу можно легко выучить по принципу, данному на сайте
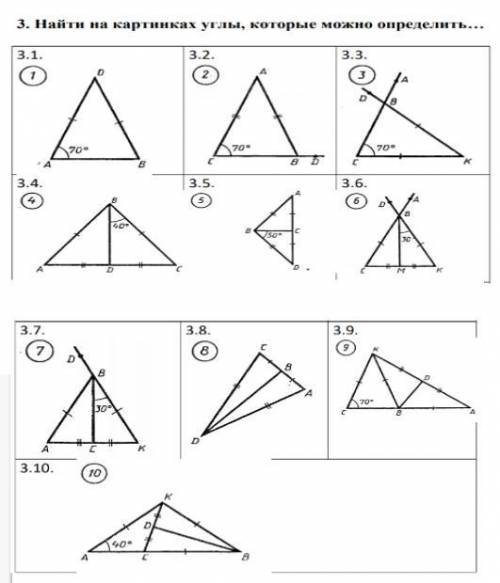
1.
А=В=70°
D=180°-(70°+70°)=40°
2.
C=B=70°
A=40°
угол ABD=180°-70°=110°
3.
C=B=70°
K=40°
ABK=180°-70°=110°
DBA=180°-110°=70°
4.
C=90°-40°=50°
C=A=50°
ABD=DBC=40°
B=40°+40°=80°
5.
D=90°-50°=40°
D=A=40°
DBC=CBA=50°
CBA=50°+50°=100°
6.
K=90°-30°=60°
K=C=60°
CBM=MBK=30°
CBK=30°+30°=60°
ABK=180°-60°=120°
DBA=180°-120°=60°
Объяснение: