Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
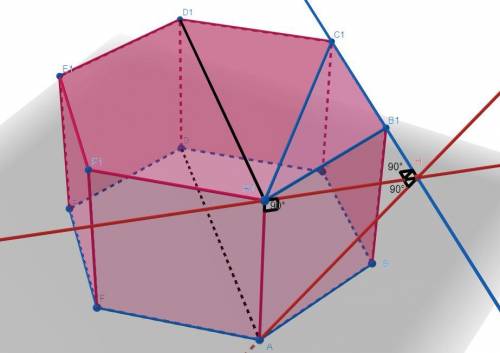
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.

A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
-----------
теперь по теореме пифагора найдем AH:
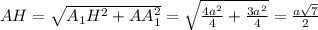
ответ: 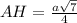
теорема: около любого треу-ка можно описать окр-ти.
док-во: рассотрим произвольный треу-ик авс.обозначим буквой о точку пересечения серединных перперндикуляров к его сторонам и проведем отрезки оа,ов и ос.т.к. точка о равноудлалена от вершин треуг-ка авс,то оа=ов=ос.паоэтому окр-ть с центром о радиуса оа проходит через все 3 вершины треу-ка и значит является описанной около треу-ка авс.теорема доказана.
все что