по формуле радиуса описанной окружности
R=5 м
a=2Rsin pi/n
n=10
a=2*5*sin pi/10=10*sin 18=10*(корень(5)-1)/4=2.5*(корень(5)-1)
1) Известно, что sin 72 = cos 18
2) 2sin 36cos 36 =cos 18
3) 4sin 18cos 18 ( 1-2sin(2) 18) =cos18
sin(2) 18 это синус квадрат 18
4)4sin 18 ( 1-2sin(2) 18) =1
5) 8sin(3) 18 - 4 sin 18 +1=0
Обозначим sin 18 =Х , тогда
6) 8х3-4х +1=0 ( левая часть раскладывается на множители)
7) ( 2х-1) ( 4х2 +2х -1) =0
х=1/2 - не подходит
8) 4х2 +2х -1=0
( решая отбирая лишь положительный коерень - он искомый)
sin 18=(корень(5)-1)/4
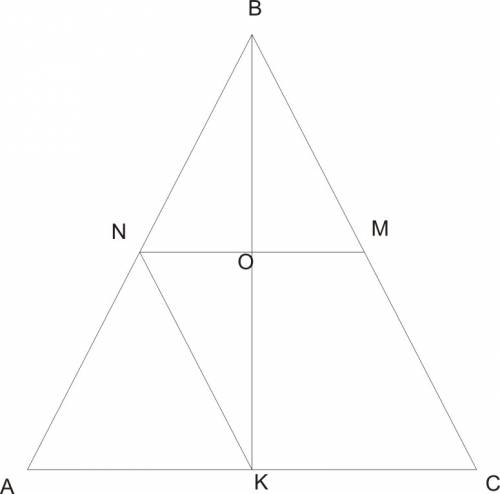
Δ АВС - равнобедренный
ВК = 30 см - биссектриса к основанию АС, она же и медиана Δ АВС ⇒ АК=КС
NM = 16 см - средняя линия II АС ⇒AN=NB
NK = ? - средняя линия II ВС
NM x ВК в т.О и деляться ей пополам, т.к. Δ NMB подобен Δ АВС по 3-м углам, ⇒ Δ NMB равнобедренный и ВО его высота, биссектриса и медиана.
ВО=ВК т.к. NM средняя линия Δ АВС
Получаем
NO=1/2NM= 16/2=8
OK=1/2ВК= 30/2=15
Δ NOK прямоугольный, т.к. уже доказано, что BO высота Δ NMB ⇒ <BON = 90°
<NOK - смежный и =180°-<BON = 90°
По теореме Пифагора находим NK - гипотенузу Δ NOK
NK=√(NO²+OK²) = √(8²+15²)=√(64+225)=√289=17 см
1) cosA=1/2; sinA - ?
(Пользуемся формулами: sin^2A+cos^2A=1)
Тогда: sin^2a=1-cos^2A
sinA=+-sqrt(1-cos^2A)
sinA=+-sqrt(1-1/4)
sinA=+-sqrt(3/4)
sinA=+-sqrt(3)/2
ответ: sinA=sqrt(3)/2; sinA=-sqrt(3)/2
2)cosA=sqrt(2)/2; sinA - ?
(Пользуемся формулами: sin^2A+cos^2A=1)
sin^2A=1-cos^2A
sinA=+-sqrt(1-cos^2A)
sinA=+-sqrt(1-2/4)
sinA=+-sqrt(1-1/2)
sinA=+-sqrt(1/2)
sinA=+-1/sqrt(2)
sinA=+-sqrt(2)/2
ответ: sinA=sqrt(2)/2; sinA=-sqrt(2)/2;
3) sinA=1/3; cos - ?
(Пользуемся формулами: sin^2A+cos^2A=1)
cos^2A=1-sin^2A;
cosA=+-sqrt(1-sin^2A);
cosA=+-sqrt(1-1/9);
cosA=+-sqrt(8/9)
cosA=+-sqrt(8)/3
cosA=+-2*sqrt(2)/3
ответ: cosA=2*sqrt(2)/3; cosA=-2*sqrt(2)/3
(Если есть вопросы. пишите в ЛС(Личные сообщения)