Основным сечением цилиндра является квадрат диагональ, которого равна 8корней из 2см.найдите объём цилиндра?

👇

Ответ:

03166

15.08.2022

Квадрат. Значит, все стороны равны. Пусть все стороны будут равны х. Рассмотрим прямоугольный треугольник (две стороны квадрата - катеты - и его диагональ - гипотенуза). По теореме Пифагора 128 = 2*х^2.

х^2 = 64

x = 8

То есть, высота цилиндра равна 8 см и радиус основания равен 8/2 = 4 см.

Находим площадь основания: п*r^2, то есть, п*16 см^2.

Ну и отсюда уже просто посчитать объем. Домножаем на высоту и получаем 128п см^3.

4,7(72 оценок)

Открыть все ответы

Ответ:

MYLITTLEPONY15

15.08.2022

а) Нет такого шестиугольника

b) Внешний угол семиугольника равен 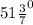$51\frac{3}{7}^0$ . Сумма внешних углов семиугольника равна 360°.

Объяснение:

а) сумма углов выпуклого многоугольника равна по формуле

S=180°(n-2)

Где n - количество углов многоугольника. Здесь n=6.

S=180°(6-2)

S=180°*4

S=720° - сумма внутренних углов шестиугольника.

Просуммируем 6 углов

10°+50°+140°+175°+185°+200°=200°+175°+185°+200°=400°+360°=760°

То есть такого выпуклого шестиугольника не существует в Евклидовой геометрии.

b) У правильного семиугольника сумма внутренних углов равна

S=180°(7-2)

S=180°*5

S=900°

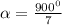$\alpha=\frac{900^0}{7}$ - внутренний угол семиугольника.

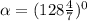
$\alpha=(128\frac{4}{7})^0$

Внешний угол равен

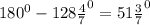
$180^0-128\frac{4}{7}^0=51\frac{3}{7}^0$

А сумма внешних углов равна

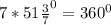$7*51\frac{3}{7}^0=360^0$ .

4,5(15 оценок)

Ответ:

Stall124

15.08.2022

Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на эту плоскость.
1) Обозначим расстояние от В до плоскости - ВС,
от М до плоскости - МН.
АС= проекция АВ на плоскость, ⇒ А, Н и С лежат на одной прямой.
Отрезки, перпендикулярные плоскости , параллельны.
Угол М=углу В как углы при пересечении параллельных МН и ВС секущей АВ, углы Н и С прямые,
угол А общий для  ∆ АМН и ∆ АВС ⇒ они подобны.
Из подобия следует АВ:АМ=ВС:МН=(2+3):2⇒
ВС:МН=5:2
МН=2•(12,5:5)=5 м
  Если АВ - перпендикуляр к плоскости, то расстояние от нее до В=12,5, а до М равно 2/5 от АВ и равно 5 м.
––––––––––––––––––––––––––––––––––––––
2)Пусть наклонные будут:
ВС=а, ВА=а+6
ВН- расстояние от общего конца В до плоскости.
Т.к. это расстояние общее, ВН⊥ плоскости, то
из прямоугольного ∆ АВН
ВН²=АВ²-АН²
из прямоугольного ∆ ВСН
ВН²=ВС²-НС²⇒
АВ²-АН²=ВС²-НС²
(а+6)²-17²=а²-7²
⇒ решив уравнение, получим
12а=204
а=17 см
ВС=17 см
АВ=17+6=23 см
–––––––––––––––––––––
3) Пусть эти опоры КМ=4 м, ТЕ=8 м, МЕ=3 м.
Т.к. обе вертикальные, то они параллельны.
Т - выше К на 4м, расстояние между К и точкой Р на ТЕ=3м,
∆ КТР с отношением катетов 3:4 - египетский ⇒ гипотенуза КТ=5 м ( проверка по т.Пифагора даст тот же результат).
ответ - 5 м.

4,7(62 оценок)

Это интересно:

Компьютеры-и-электроника

19.09.2020

Как распечатать Google Календарь...

Путешествия

23.11.2022

Как безопасно путешествовать по Южной Африке...

Компьютеры-и-электроника

12.03.2021

Как подготовить кабель Ethernet и объединить два ноутбука в сеть...

Компьютеры-и-электроника