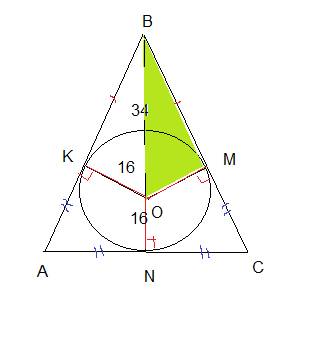
Стороны треугольника являются касательными к окружности.
Касательная перпендикулярна радиусу, проведенному в точку касания.
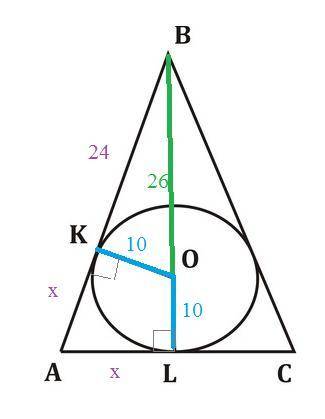
ОК⊥АВ
OL⊥AC
Высота равнобедренного треугольника, проведённая к основанию, одновременно и медиана и биссектриса.
AL=LC
ОК=ОL=10 см
BO=26 см
По теореме Пифагора
BK²=BO²-OK²=26²-10²=676-100=576
BK=24 см
Пусть AK=x
По свойству касательных, проведенных к окружности из одной точки
AK=AL=x
По теореме Пифагора из прямоугольного треугольника АВL:
AB²-AL²=BL²
(24+x)²-x²=(10+26)²
24²+48x+x²-x²=36²
48x=720
x=15
AC=2AL=30 см
S(Δ ABC)=(1/2)AC·BL=(1/2)·30·36=540 кв см.
200π√3 см²
Объяснение:
Дано:
Цилиндр
О1А=20см
<О1АО=60°
Sбок=?
Решение.
cos60°=OA/O1A
1/2=OA/20
OA=20/2=10см радиус цилиндра.
Теорема Пифагора.
ОО1²=О1А²-ОА²=20²-10²=400-100=300
ОО1=√300=10√3см высота цилиндра.
Sбок=2πRh
Sбок=2π*ОА*ОО1=2*π*10*10√3=
=200π√3 см²