Первый .
Для решения применим теорему косинусов для треугольника.
ВС2 = АВ2 + АС2 – 2 * АВ * ВС * CosA.
ВС2 = 9 + 36 – 2 * 3 * 6 * (1 / 2).
ВС2 = 45 – 18 = 27.
ВС = √27 = 3 * √3 см.
Второй .
Проведем высоту ВН.
В прямоугольном треугольнике АВН катет АН лежит против угла 300, тогда АН = АВ / 2 = 3 / 2 = 1,5 см. СН = АС – АН = 6 – 1,5 = 4,5 см.
Тогда ВН2 = АВ2 – АН2 = 9 – 2,25 = 6,75.
В прямоугольном треугольнике ВСН, ВС2 = ВН2 + СН2 = 6,75 + 20,25 = 27.
ВС = √27 = 3 * √3 см.
ответ: Длина стороны ВС равна ВС 3 * √3 см.
Объяснение:
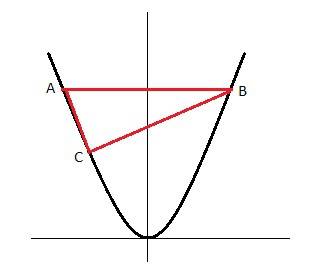
BE=6см, P=22.5см
Объяснение:
△ABC и △BEK подобны, т.к. при параллельных AC и EK у них равны соответственные углы.
Значит их стороны и периметры относятся к друг другу с коэф-том подобия k=AC/EK=12/9=4/3
Тогда AB/BE=k BE=AB/k=8*3/4=6
P(ABC)/P(BEK)=k P(BEK)=P(ABC)/k=(8+10+12)*3/4=22.5