В параллелограмме ABCD проведена диагональ АС. Точка О является центром окружности, вписанной в треугольник АВС. Расстояния от точки О до точки А и прямых AD и AC равны соответственно 10, 8 и 6. А) Докажите, что ABCD – прямоугольник
Б) Найдите площадь параллелограмма ABCD
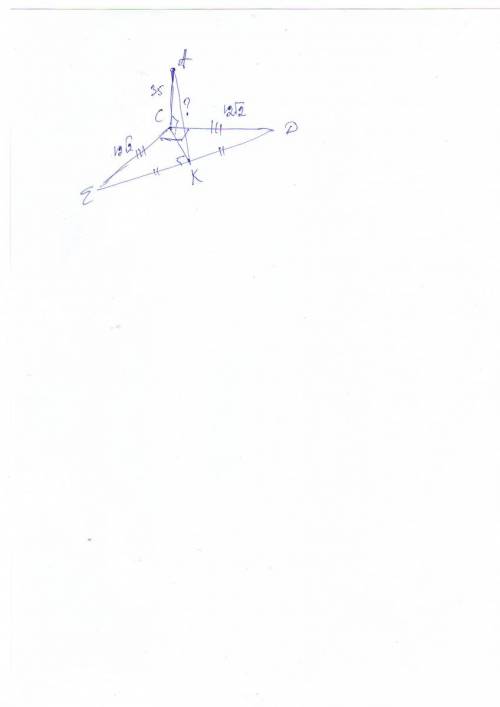
Катет ВО равен 4√2 как половина диагонали квадрата (это основание пирамиды со стороной 8):
SO = √(6² - (4√2)²) = √(36-32) = √4 = 2.
Так как отрезок МК параллелен диагонали АД, то он отсекает на высоте одну третью часть (свойство подобных треугольников), которая равна:
ОР = (1/3)*2 = 2/3.
Угол ВОР - это угол пересечения заданных плоскостей (угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях).
Тангенс этого угла равен tg α = (2/3) / (4√2) = 1 /(6√2) = 0,117851.
Угол равен arc tg 0,117851 = 0,11731 радиан = 6,721369°.