40. 1) Нет, не могут. Углы в 110° и 92° - тупые, а в треугольнике не может быть двух тупых углов (следствие из теоремы о сумме углов треугольника).
2) Да, могут. Угол в 78° - острый, а в 101° - тупой. В треугольнике может быть тупой и острый угол.
(Даже можем сделать проверку. Если мы сложим эти углы (101°+78°), то в сумме получим 179°. Получается, что третий угол равен 1°. Это вполне может быть.)
3) Нет, не могут. Опять же, давайте-ка сразу сложим эти углы. 93°+88° = 181°. Такого категорически не может быть! Сумма двух углов не может превосходить 180°. То есть, получается, что третий угол равен -1°? Такого, опять же, не может быть. Градусная мера угла - строго положительная величина.
4) Нет, не могут. Опять же, сложим эти углы. 170°+12° = 182°. Этого не может быть, так как сумма трёх углов треугольника равна 180°.
ответ: 2).
Объяснение: в правильной 3-хугольной, 4-хугольной и 6-угольной призме все стороны основания равны. Для того чтобы найти объём каждой призмы воспользуемся формулой: V=Sосн×h, где h- её высота т.е. боковое ребро=12
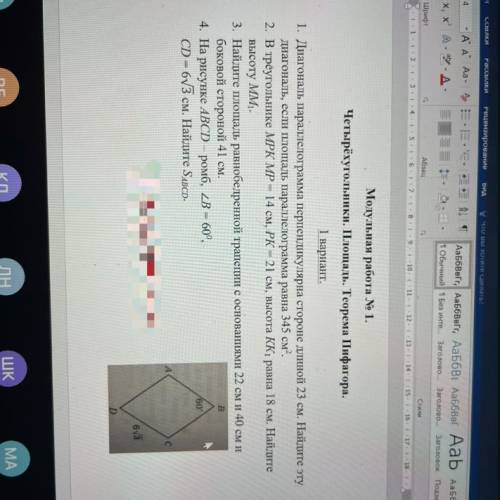
ЗАДАНИЕ 1
Найдём площадь основания 3-хугольной призмы, (где основанием является равносторонний треугольник) по формуле: S=a²√3/4, где а - сторона основания:
Sосн=10²√3/4=100√3/4=25√3(ед²)
Теперь найдём объем:
V=25√3×12=300(ед³)
ОТВЕТ: V=300(ед³)
ЗАДАНИЕ 2
Так как в основании правильной четырёхугольной призмы лежит квадрат, то его площадь вычисляется по формуле: S=a², где а - его сторона:
Sосн=10²=100(ед²)
V=100×12=1200(ед³)
ОТВЕТ: V=1200(ед³)
ЗАДАНИЕ 3
В основании правильной 6-угольной призмы лежит правильный шестиугольник. Его площадь состоит из 6 равносторонних треугольников. Найдём площадь одного такого треугольника по формуле:
S=a²√3/4=10²√3/4=100√3/4=25√3(ед²)
Так как таких треугольников 6 то, площадь основания=
Sосн=25√3×6=150√3(ед²)
Теперь найдём объем призмы:
V=150√3×12=1800(ед³)
ОТВЕТ: V=1800(ед³)