а) боковая сторона равна 4√3 см;
б) медиана, проведённая к основанию, равна 2√3 см;
в) медиана, проведённая к боковой стороне, равна 2√21 см.
Объяснение:
Дано:
ΔАВС:
АВ = ВС - боковые стороны
АС = 12 см - основание
∠А = ∠С = 30° - углы при основании
Найти:
а) АВ - боковую сторону
б) ВМ - медиану, проведённую к основанию
в) АК - медиану, проведённую к боковой стороне
а)
В равнобедренном треугольнике медиана, проведённая к основанию, делит основание пополам, то есть
АМ = СМ =0,5АС = 6 см;
и является высотой, поэтому ΔАВМ - прямоугольный с углом
∠ВМА = 90°.
Тогда
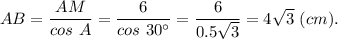
и
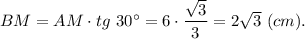
в)
В ΔАВС: ∠В = 180° - 2 · 30° = 120°
Рассмотрим ΔАВК.
АВ = 4√3 см; ВК = 0,5 ВС = 2√3 см; ∠В = 120°.
По теореме косинусов найдём ВК
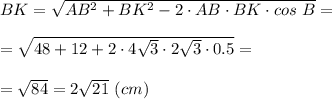
2. Циркулем откладываем на этой прямой 3 равных отрезка так, чтобы они в сумме были длиннее, чем исходный отрезок. Получаем точки B, C, D, E, причем [BC]=[CD]=[DE], как радиусы окружностей, и [BE] > [KN]
3. Через начало первого отрезка и через конец последнего проводим 2 прямые, соединяющие эти точки с началом и концом данного отрезка. - Прямые (BK) и (EN)
4 Так как новый отрезок длиннее, чем данный, то эти прямые пересекутся в некоторой точке А. Таким образом, получится треугольник ABE с вершиной в точке А. Из этой точки строим 2 луча, пересекающие прямую а в точках C и D, которые мы отметили циркулем. Тогда на данном отрезке получатся 2 точки F и S, которые разобьют его на 3 равные части. То есть [KF]=[FS]=[SN]= 1/3[KN]