R = 4см. АВ = CD = 4√2 см.
Объяснение:
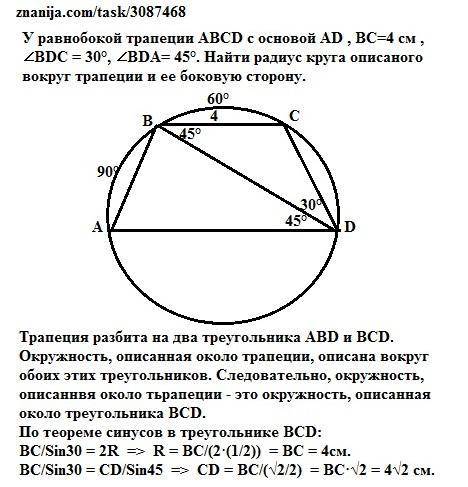
Трапеция разбита на два треугольника ABD и BСD. Окружность, описанная около трапеции, описана вокруг обоих этих треугольников. Следовательно, окружность, описаннвя около тьрапеции - это окружность, описанная около треугольника ВСD.
∠CBD = ∠BDA = 45° как внутренние еакрест лежащие углы при параллельных AD и ВС и секущей BD.
По теореме синусов в треугольнике ВСD:
ВС/Sin30 = 2R => R = BC/(2·(1/2)) = ВC = 4см.
ВС/Sin30 = СD/Sin45 => CD = BC/(√2/2) = ВC·√2 = 4√2 см.
S=1/2*a*b*Sinγ
S=1/2*2*10*Sin45 = 1/2*20*(√2/2)=5√2