Рассмотрим треугольник АВС. Он равнобедренный по условию, так как боковые стороны у него равны. Значит, углы при основании тоже равны - по свойству равнобедренного треугольника.
Так как по условию треугольник АВС ещё и прямоугольный, то сумма его острых углов даёт 90° - по свойству прямоугольного треугольника.
Найдем углы при основании:
BAC = ACB = 90° : 2 = 45°.
Далее рассмотрим углы АСВ и ЕСD - они вертикальные, значит АСВ = ЕСD = 45°.
Так как треугольник СЕD по условию тоже равнобедренный (боковые стороны у него равны по условию), то углы при основании равны. Отсюда находим угол СЕD, он же угол х:
(180° - угол ЕСD) : 2
(180° - 45°) : 2 = 67,5° - угол х.
1-б 2-д 3-а 4-в
Объяснение:
Трапеция равносторонняя, диагональ делит угол на пополам и эта же половинка угла будет в треугольнике ABC ∠C => ABC равнобедренный. То есть бочные стороны и меньшая основа равны => x+x+x+12=52 находим что x=10. Отсюда находим большую основу, средняя линия это меньшая основа+большая основа/2 (10+22)/2=16. Рисуем 2 высоты, видим что большая основа поделилась на 3 отрезка, центральный из них равен меньшей основе, то есть 10. Понимаем что 2 других отрезка равны 12 см, а значит каждый из них по 6. За теоремой пифагора ищем высоту (любую), она будет являться катетом, обозначим как x. 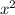 =
=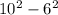 , x=8
, x=8
Подібні
Объяснение: