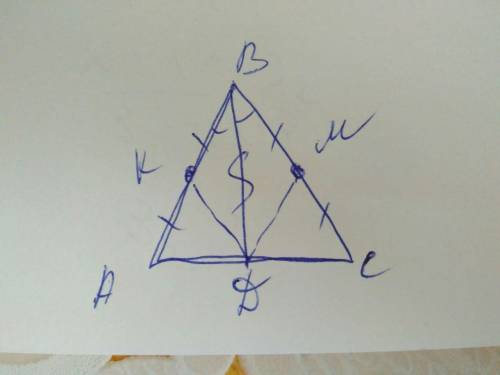
Дано: ΔАВС - равнобедренный, АК = КВ = ВМ = МС (т. К и М - середины боковых сорон АВ и СВ соответственно), ВD - медиана.
Доказать: ΔBKD = ΔBMD.
Доказательство: есть два треугольника BKD и BMD, у которых сторона BD - общая. стороны KB и BM - равны, т.к. ΔABC - равнобедренный, а точки K и M - середины сторон АВ и СВ соответственно. Т.к. BD - медиана равнобедренного ΔABC, то ∠KBD = ∠DBM. Следовательно, по первому признаку равенства треугольников (если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны), треугольники BKD и BMD равны, т.к. KB = BM, BD - общая сторона, ∠KBD = ∠DBM.
Чтд.
по свойству пересекающихся хорд произведение отрезков одной хорды равно произведению отрезков другой хорды. АК*КВ=СК*КД
АВ=10+6=16 см, СД=16+3=19см.
пусть СК=х, тогда КД=19-х
10*6=х*(19-х)
60=19х-х^2
x^2-19x+60=0
x=15, x=4
если СК=15, то КД=19-15=4см
если СК=4, то КД=19-4=15см
ответ 15см и 4см