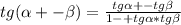Докажите,что в павнобедренном треугольнике отрезок,соединяющий любую точку основания,отличную от вершины,с противоположной вершиной,меньше бокоой стороны

👇

Ответ:

makssaulin

24.07.2021

В треугольнике чем больше противолежащий угол - тем длиннее сторона.

Либо опускаем высоту и рассматриваем получившиеся треугольники с катетами являющимися высотами. Длину гипотенузы рассчитываем по теореме Пифагора. Чем меньше расстояние от точки пересечения высотой основания исходного треугольника до выбранной точки (длина второго катета), тем меньше гипотенуза.

4,8(22 оценок)

Открыть все ответы

Ответ:

mishaniy

24.07.2021

В квадрате диагонали перпендикулярны друг другу.
Если есть точка М(х₁ у₁) и прямая Ах + Ву + С = 0, то уравнение перпендикулярной прямой: А(у - у₁) - В(х - х₁) = 0.
Подставляем известные данные: точка А(5;-4) и прямая - диагональ ВД: х - 7у - 8 = 0.
Уравнение диагонали АС: 1*(у - (-4)) - (-7)*(х - 5) = 0.
у + 4 + 7х - 35 = 0,
АС: 7х + у - 31 = 0.
Эта же прямая в виду уравнения с коэффициентом:
у = -7х + 31.

В уравнении типа у = кх + в коэффициент к - это тангенс угла наклона прямой к оси "х".
Стороны квадрата проходят под углом +45° и -45° к диагонали.
Используем формулу тангенса суммы (разности) углов:
$tg( \alpha +- \beta )= \frac{tg \alpha +-tg \beta }{1-+tg \alpha *tg \beta }$ .
Используя к = -7 для АС, находим "к" для сторон АВ и АД:
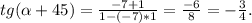
$tg( \alpha +45)= \frac{-7+1}{1-(-7)*1} = \frac{-6}{8} =- \frac{3}{4} .$
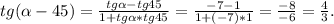
$tg( \alpha -45)= \frac{tg \alpha -tg45}{1+tg \alpha *tg45} = \frac{-7-1}{1+(-7)*1}= \frac{-8}{-6}= \frac{4}{3}.$

Теперь переходим к уравнениям сторон.
У параллельных прямых коэффициент к одинаков.
Найдём координаты точки С, симметричной точка А относительно прямой ВД.
Алгоритм решения :
1) Находим прямую (диагональ АС), которая перпендикулярна прямой ВД.
2) Находим точку К пересечения прямых - это будет центр квадрата.
3) Точка К является серединой отрезка АС. Нам известны координаты середины и одного из концов. По формулам координат середины отрезка находим точку С.

1) Уравнение АС найдено.
2) ВД: х - 7у - 8 = 0 -7х + 49у + 56 = 0
АС: 7х + у - 31 = 0 7х + у - 31 = 0
--------------------------
50у + 25 = 0
у = -25 / 50 = -1/2.
х = 7у + 8 = 7*(-1/2) + 8 = -3,5 + 8 = 4,5.
Получили координаты точки К(4,5; -0,5).

3) Хс = 2Хк - Ха = 2*4,5 - 5 = 9 - 5 = 4.
Ус = 2Ук - Уа = 2*(-0,5) - (-4) = -1 + 4 = 3.

Уравнения сторон:
АВ: -4 = (-3/4)*5 + в в = -4 + (15/4) = (-16/4) + (15/4) = -1/4.
АВ: у = (-3/4)х - (1/4).

СД: 3 = (-3/4)*4 + в в = 3 + (12/4) = 3 + 3 = 6.
СД: у = (-3/4)х + 6.

АД: -4 = (4/3)*5 + в в = -4 - (20/3) = (-12/3) - (20/3) = -32/3
АД: у = (4/3)х - (32/3).

ВС: 3 = (4/3)*4 + в в= 3 - (6/3) = (9 - 16)/3 = -7/3.
ВС: у = (4/3)х - (7/3).

4,8(72 оценок)

Ответ:

znaika757

24.07.2021

У меня получилось что расстояние от точки М до вершины В равно 8 см, показываю как получил:

1. СК и АN - медианы треугольника АВС.

2. По условию задачи точка М удалена от стороны АС на 4 см, то есть она принадлежит перпендикуляру, проведенному к стороне АС.

3. Проведем через эту точку высоту ВН к стороне АС.

4. По условию задачи треугольник АВС равнобедренный, следовательно, высота ВН является еще и медианой.

5. Точка пересечения медиан, согласно их свойствам, делит каждую из них на два отрезка, относящихся как 2 : 1, начиная от вершины, то есть ВМ : НМ = 2 : 1.

ВМ = 4 х 2 = 8 см.

ответ: расстояние от точки М до точки В равно 8 см.

4,5(47 оценок)

Это интересно:

Семейная-жизнь

11.01.2022

Как рассказать парню о беременности после случайного секса?...

Здоровье

12.08.2021

Избавление от боли в зубе мудрости: легкий и безболезненный способ...

Компьютеры-и-электроника

14.06.2022