
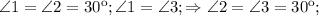 )
) 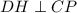 ,
, 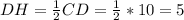 как катет лежащий против угла 30 в треугольнике CHD.
как катет лежащий против угла 30 в треугольнике CHD. 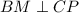 ,
, 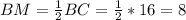 как катет лежащий против угла 30 в треугольнике BMC.
как катет лежащий против угла 30 в треугольнике BMC. 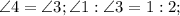
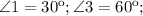 Тогда в ромбе
Тогда в ромбе 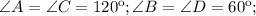
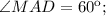 , тогда
, тогда 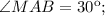 Треугольник BAM равнобедренный, АВ=АМ, тогда
Треугольник BAM равнобедренный, АВ=АМ, тогда 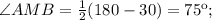
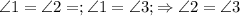 , треугольник MCD равнобедренный, MD=CD=3,
, треугольник MCD равнобедренный, MD=CD=3, 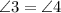 ,
, 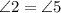 , как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.
, как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.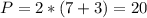 .
.
8 см; √15 см
Объяснение:
Дано: ΔАВС, АС=√24 см, АН=3 см. Найти СН и АВ.
ΔАСН - прямоугольный. По теореме Пифагора
СН²=АС²-АН²=(√24)²-3²=24-9=15 см; СН=√15 см
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
СН²=АН*ВН; 15=3*ВН; ВН=5 см.
АВ=АН+ВН=3+5=8 см