
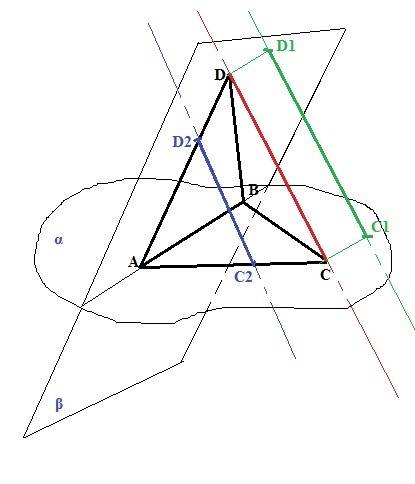
Есть теорема: "Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость". Отрезок CD имеет общую точку C с плоскостью АВС и общую точку D с плоскостью ABD. Через две точки можно провести только одну прямую, следовательно, прямая, содержащая отрезок СD, пересекает плоскость, содержащую треугольник АВС и плоскость, содержващую треугольник ABD. Значит любая прямая, параллельная СD, по приведенной теореме, также пересечет и плоскость АВС и плолскость ABD. Что и требовалось доказать.
∠T=∠P (усл.)
TO=PO (усл)
∠POH=∠TOG (как вертикальные)
⇒ ΔPOH=ΔTOG по стороне и двум прилежащим к ней углам ⇒ GO=OH как соответственные элементы ⇒ ΔGOH - равнобедренный по определению.
Объяснение:
УДАЧИ!