Sc = d²·tgα·√2/(2+tgα).
Sб = 4d²·tgα/(2+tgα).
So = d²/(2+tgα).
So =
Объяснение:
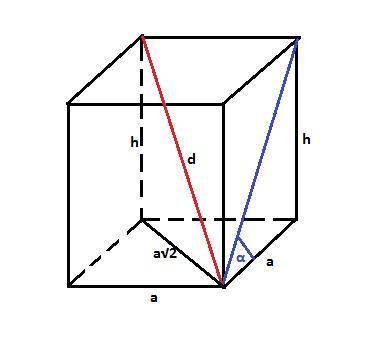
Призма правильная, значит в основании лежит квадрат. Пусть сторона квадрата равна "а". Тогда диагональ квадрата равна а√2.
Высота призмы равна h = a·tgα (из прямоугольного треугольника - половины боковой грани).
Квадрат диагонали призмы d² = h²+2a². (из прямоугольного треугольника - половины диагонального сечения).
d² = a²·tg²α+2a² = a²(2+tgα). => a = d/(√((2+tgα)).
h = a·tgα = d·tgα/(√((2+tgα)).
Тогда площадь диагонального сечения равна:
Sc = a√2·h = d√2/(√(2+tgα))·dtgα/(√(2+tgα)) = d²·tgα·√2/(2+tgα).
Площадь боковой поверхности равна произведению периметра основания на высоту призмы:
Sб = 4·a·h = 4d/(√((2+tgα))·d·tgα/(√((2+tgα)) = 4d²·tgα/(2+tgα).
Площадь основания (квадрата) равна квадрату стороны:
So = a² = d²/(2+tgα).
a ∩ b.
Один из углов в 4 раза > другого.
Найти :Больший угол = ?
Решение :При пересечении двух прямых образуются четыре угла.
∠1 = ∠3, ∠2 = ∠4 (это пары вертикальных углов. Они равны между собой по свойству вертикальных углов).
Пусть ∠2 = х.
Тогда, по условию задачи, один из углов должен быть равен 4х.
Естественно, что ∠4 ≠ 4х, так как уже ∠4 = х по выше сказанному.
Тогда пусть ∠1 = 4х.
∠1 и ∠2 - смежные (по определению).
Сумма смежных углов равна 180°.Отсюда :
∠1 + ∠2 = 180°
4х + х = 180°
5х = 180° ⇒ х = 180° : 5 = 36°
4х = 4*36° = 144°.
(Естественно, что за 4х мы брали самый больший угол, поэтому в ответ пойдёт значение 4х).
ответ :144°.