Объяснение: Подробно - см. рисунок.
Смежные (соседние) стороны многоугольника, а ромб - параллелограмм и в то же время многоугольник - имеют общую вершину. Обозначим ромб АВСD. Стороны ромба равны, его диагонали –биссектрисы его углов и пересекаются под прямым углом.
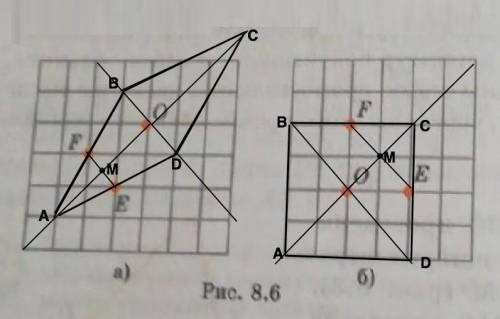
а) Соединим т.F и т.Е. Отрезок FE делит стороны пополам (дано), он – средняя линия половины ромба - равнобедренного ∆ АВD. => EF делит пополам и его биссектрису АО ( высоту, медиану). Точка М - пересечение прямой АО и FE ( пересечение диагоналей квадратной клетки, через которую проходит FE).
Отметим на луче ОА отрезок МА=ОМ, продлим диагональ в другую сторону на длину ОА.Через т. О проведем прямую ВD перпендикулярно АС ( через противоположные вершины соседних квадратных клеток) и отметим на ней ОВ=2•FM и OD=2•ME. Диагонали ромба построены. Соединив точки А, В, С и D, получим нужный ромб.
б) Аналогично восстанавливается ромб по второй задаче. Здесь получится квадрат – ромб, в котором диагонали равны и все углы прямые .
task/29635078 Дан параллелограмм ABCD , F – точка пересечения диагоналей , О – произвольная точка пространства. Доказать: 1) (OA) ⃗+(OC) ⃗=(OB) ⃗+ (OD) ⃗ ; 2) (OF) ⃗=1/4((OA) ⃗+(OB) ⃗+(OC) ⃗+(OD) ⃗) .
Решение : Если векторы исходят из одной точки , то вектор суммы исходит из общей начальной точки векторов и является диагональю параллелограмма, сторонами которого являются данные векторы . * * * ( Сумма векторов , правило параллелограмма ) * * *
1) (OA) ⃗+ (OC) ⃗ =2*(OF) ⃗ и (OB) ⃗+(OD) ⃗ = 2*(OF) ⃗
значит (OA) ⃗+ (OC) ⃗ = (OB) ⃗+(OD) ⃗
2) (1/4) * [ (OA) ⃗+(OB) ⃗+ (OC) ⃗+(OD) ⃗] =
(1/4) * [ (OA) ⃗+ (OC) ⃗+(OB) ⃗+(OD) ⃗] =
(1/4) * [ 2*(OF) ⃗+2*(OF) ] =
(1/4) * 4*(OF) ⃗ = (OF) ⃗ .
вот так же или нет или не правилно Мори или правилно лаик