Определите вид четырехугольника АВСD (параллелограмм, прямоугольник, ромб, квадрат), если: А (2; 3), В (3; 5), С (4; 3), D (3; 1).
Объяснение:
d=√( (х₁-х₂)²+(у₁-у₂)²), где (х₁;у₁), (х₂;у₂) -координаты концов отрезка.
АВ=√(1²+2²)=√5, ВС=√(1²+(-2)²)=√5, СD=√( (-1)²+(-2)²)=√5,
АD=√(1²+(-2)²)=√5 ⇒все стороны равны, значит это либо ромб , либо квадрат.
Найдем угол между сторонами ВА и ВС .
Найдем координаты вектора ВА(-1; -2) , ВС(1 ;-2).
cos(BA;ВС)=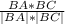 
cos(BA;ВС)=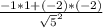
= 
⇒ это ромб , т.к у квадрата угол 90° (cos 90°=0)
" Доказать, что биссектрисы двух углов с соответственно перпендикулярными сторонами парралельны, принадлежат одной прямой или взаимно перпендикулярны. все варианти я решил(а), но меня интересует вариант принадлежат одной прямой. Нужно доказательство именно этого варианта "
Объяснение:
Данные углы образуют четырехугольник, противоположные углы которого в сумме дают 180°.
Пусть для определенности МС⊥АС, МВ⊥АВ и АМ- биссектриса ∠САВ . Тогда около 4-х угольника АВМС можно описать окружность , т.к. ∠АСМ+∠АВМ=180° и АМ-диаметр .
Т.к. МС⊥АС, МВ⊥АВ , то М- равноудалена от сторон АС и АВ ∠САВ . Тогда ΔАСМ=ΔАВМ как прямоугольные по катету и гипотенузе⇒ соответственные элементы равны ⇒∠СМА=∠АВМ⇒ МА биссектриса ∠СМВ.