ответ: πa²
Объяснение: 1)Для нахождения радиуса описанной окружности трапеции делают дополнительные построения — строят диагональ трапеции BD и высоту ВМ. Теперь трапеция разбита на два треугольника ABD и BСD. Окружность при этом описана вокруг обоих этих треугольников. Далее по данным параметрам трапеции находим диагональ BD, высоту BM и по формуле вычисления радиуса описанной окружности около треугольника R=abc/4S ⇒ Трапеция ABCD у нас равнобокая, большее основание АD =2а, меньшее ВС=а, боковые стороны АВ=СD=a 2) АМ= (2а-а)/2=а/2 ; MD= 2a - a/2= 3a/2 3) из ΔАВМ имеем: ВМ²=h²= a² - (a/2)²=3a²/4 ⇒ h=a√3/2 4) из ΔМВD имеем: BD²= BM²+MD²= 3a²/4+ 9a²/4 = 3a², ⇒ BD=a√3. 5) Площадь ΔABD равна S= 1/2·AD·BM/2 = 2a · a√3/4 = a²√3/2 ⇒ радиус окружности, описанной около ΔABD(а значит и трапеции) R= abc/4S = AB·BD·AD /4S= (a·a√3·2a) / (4·a²√3/2) = a, т.е. R=a 6) Площадь круга S₁= π·R²=π·a²
ВС=4√3см, <А=60°, <В=30°
Объяснение:
найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=8²–4²=64–16=48=4√3см
Теперь найдём <А, используя косинус угла. Косинус угла - это отношение противолежащего к углу катета к гипотенузе поэтому:
cosA=AC/AB=4/8=1/2=60°
Сумма острых углов прямоугольного треугольника составляет 90°, поэтому <В=90–60=30°
Задание 4, которое было на фото вместе остальными
Если <А=26°, то <В=90–26=64°. Найдём катет АС используя косинус угла:
AC=AB×cos26°=10×0,8988=8,988см
ВС=АВ×cos64°=10×0,4384=4,384см
ответ: ВС=4,384, АС=8,988, <В=64°
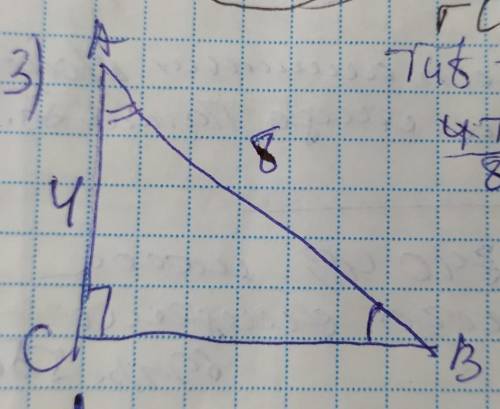
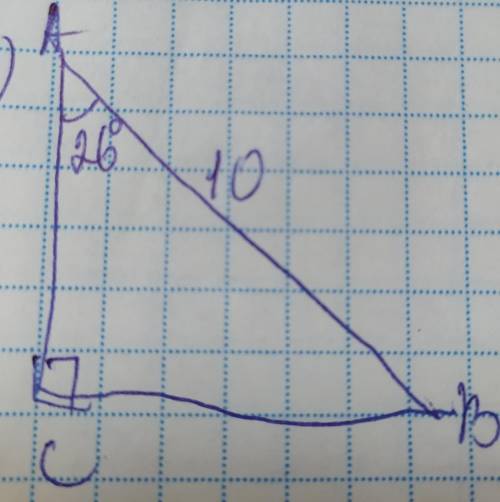
cosα=AB/SA=CD/SA=6/10=0.6