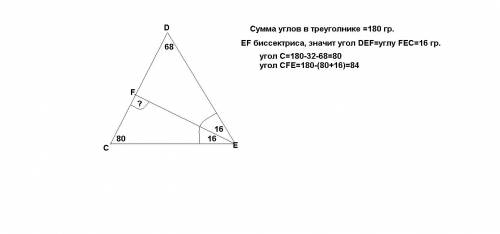
На прямой "а" откладываем циркулем произвольный отрезок АВ. Из концов этого отрезка А и В, как из центров, радиусом R=AB чертим дуги окружностей. В точках пересечения этих дуг обозначаем точку С. Угол САВ равен 60°, так как треугольник АВС равносторонний по построению.
Или так (что практически то же самое):1. К прямой "а" восстановим перпендикуляр из произвольной точки. Для этого проведем две окружности одинаковых радиусов R с центрами в произвольных точках А и В. Соединив точки пересечения этих окружностей, получим перпендикуляр к прямой "а", так как общая хорда пересекающихся окружностей перпендикулярна прямой, проходящей через центры этих окружностей. 2. Отметим на прямой "а" точку Н основания полученного перпендикуляра. Из точки А как из центра, проведем окружночть радиусом R=2АН=АВ (так как радиусы окружностей одинаковы - перпендикуляр делит отрезок АВ пополам) и соединим точку А с точкой пересечения С этой окружности и перпендикуляра. Угол АСН=30°, как угол, лежащий против катета, равного половине гипотенузы. Следовательно, угол САВ = 60° (так как сумма острых углов прямоугольного треугольника равна 90°)

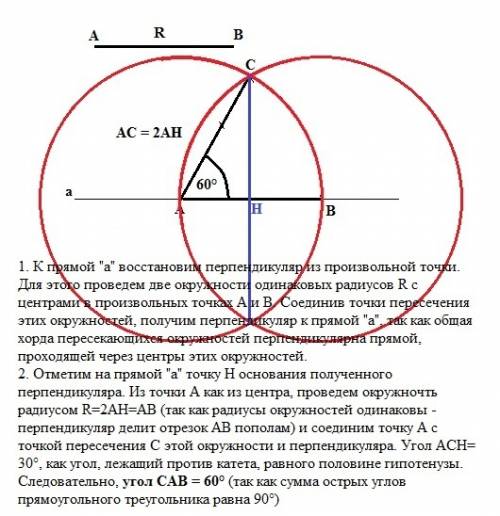
1) Угол Д=68, угол Е=32 следовательно угол С=180-68-32=80
2) ЕФ-бис-са то есть угол ФЕС и угол ДЕФ равны и равны 32:2=16
3) угол С=80(пункт 1); угол ФЕС=16 следовательно угол СФЕ=180-80-16=84
ответ: 84 градуса