Так как дано, что многоугольник выпуклый, то сумма его внешних углов равна 360 градусам.
Каждый внешний угол равен по 90 градусам, тогда мы сможем узнать количество сторон. Для этого поделим сумму внешних углов на градусную меру каждого угла - 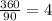
Итак, количество сторон = 4.
Но так как каждый внешний угол прямой, то и внутренние углы этого многоугольника тоже прямые. Тогда получается, что этот многоугольник - прямоугольник (все углы равны между собой).
Но так как у этого многоугольника равны все стороны (по условию) и углы, то это правильный четырёхугольник - квадрат.
ответ: квадрат.
Так как дано, что многоугольник выпуклый, то сумма его внешних углов равна 360 градусам.
Каждый внешний угол равен по 90 градусам, тогда мы сможем узнать количество сторон. Для этого поделим сумму внешних углов на градусную меру каждого угла - 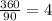
Итак, количество сторон = 4.
Но так как каждый внешний угол прямой, то и внутренние углы этого многоугольника тоже прямые. Тогда получается, что этот многоугольник - прямоугольник (все углы равны между собой).
Но так как у этого многоугольника равны все стороны (по условию) и углы, то это правильный четырёхугольник - квадрат.
ответ: квадрат.
Відповідь:
Пояснення:
Теорема о трех перпендикулярах: Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной.
AC⊥BC, т. к. ABC− прямоугольний треугольник и
PA⊥BC, т. к. перпендикуляр к плоскости треугольника ⇒CP⊥BC
значит, PCB= 90° .