Находим АВ:
АВ=√(АС²+ВС²)=√(12²+5²)=13 см
S ΔАВС=12*5/3=30 см²
полупериметр ΔАВС равен
p=(12+13+5)/2=15 cм
Радиус вписанной окружности определяется соотношением:
r=S/p=30/15=2 см
(На рисунке радиусы обозначены красным, там получится квадрат со стороной 2 см, одну букву можешь сам дописать; и писать этого всего в решении не надо)
Искомое расстояние (АО) равно:
АО=√(АК²+КО²)=√(10²+2²)=√104=2√26 см
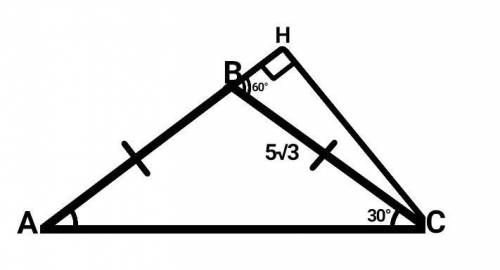
Дано :
∆АВС — равнобедренный (АС — основание).
АВ = ВС = 5√3.
<С = 30°.
СН — высота.
Найти :
СН = ?
В равнобедренном треугольнике углы при основании равны.Следовательно —
<А = <С = 30°.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.То есть —
Внешний <В = <А + <С
Внешний <В = 30° + 30°
Внешний <В = 60°.
Рассмотрим прямоугольный ∆ВСН (СН лежит вне треугольника, так как ∆АВС — тупоугольный).
BC — гипотенуза (так как лежит против угла в 90°).
Тогда —
Sin(<HBC) = CH/BC (по определению синуса острого угла прямоугольного треугольника)
Sin(60°) = CH/(5√3)
Обозначим СН за х.
Тогда —
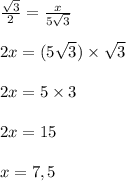
СН = 7,5 (ед).
7,5 (ед).
— — —
Надеюсь, я Вам. Есть вопросы по поводу решения? Задавайте в комментариях.
Найдём гипотенузу из Пифагоровой тройки 5 12 и 13. Гипотенуза 13.
Центр вписанной окружности- это точка пересечения биссектрис.
Найдём радиус r=s\p где р- полупериметр r=12*5\2*15=2
2. Окружность касается катетов в точке отстоящей от меньшего острого угла на 9 см. Из прямоугольных треугольников находим расстояния . Они являются гипотенузами в прямоугольных треугольниках.
Корень из 81 +4 т.е корень из 85 (это от меньшего угла)